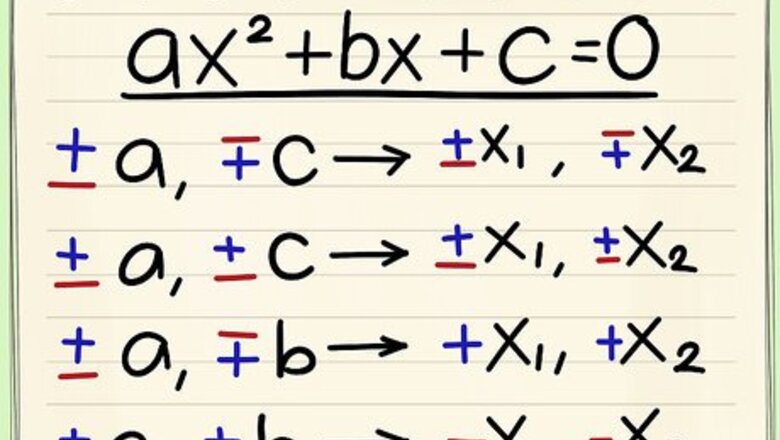
views
It uses 3 features in its solving process:
The Rule of Signs for Real Roots of a quadratic equation to look for a better solving approach.
The Diagonal Sum Method to solve simplified quadratic equations type x^2 + bx + c = 0, when a = 1. This method can immediately obtain the 2 real roots of the equation.
The transformation of a quadratic equation in standard form ax^2 + bx + c = 0 into the simplified form, with a = 1, to make the solving process much easier.
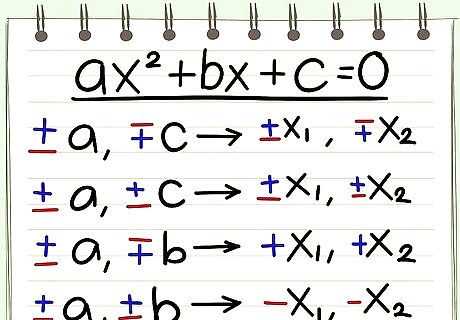
Recall the Rule of Signs. If a and c have different signs, roots have different signs If a and c have same sign, roots have same sign. If a and b have different signs, both roots are positive. If a and b have same sign, both roots are negative.
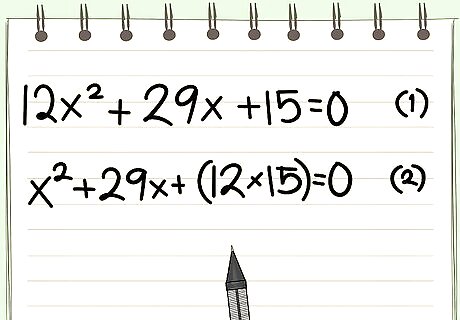
Transform the equation in standard form ax^2 + bx + c = 0 (1) into a new equation, with a = 1, and the constant C = a*c. The new equation has the form: x^2 + bx + a*c = 0, (2).
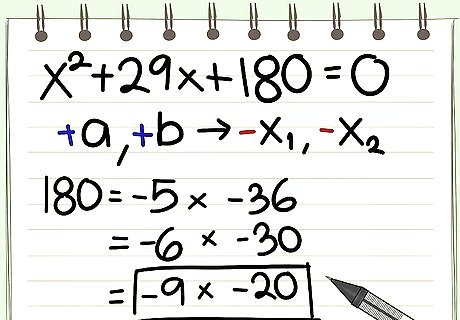
Solve the transformed equation (2) by the Diagonal Sum Method that can immediately obtain the 2 real roots. Solving results in finding 2 numbers knowing the sum (-b) and the product (a*c). Compose factor pairs of a*c following these 2 Tips below. Find the pair that equals to (-b), or b. If you can't find this pair, this means the equation can't be factored, and you should probably solve it by the Quadratic Formula. If roots have different signs (a and c different signs), compose factor pairs of a*c with all first numbers being negative. If roots have same sign (a and c same sign), compose factor pairs of a*c: with all negative numbers when both roots are negative. with all positive numbers when both roots are positive. Example 1. Solve: x^2 - 11x - 102 = 0. Roots have different signs. Compose factor pairs of c = -102 with all first numbers being negative. Proceeding: (-1, 102)(-2, 51)(-3, 34)(--6, 17). This last sum is: 17 - 6 = 11 = -b. Then, the 2 real roots are: -6 and 17. No factoring and solving binomials. Example 2. Solve: x^2 + 39x + 108 = 0. Both roots are negative. Compose factor pairs of c = 108 with all negative numbers. Proceeding: (-1, -108)(-2, -54)(-3, -36). This last sum is -39 = -b. Then, the 2 real roots are: -3, and -36. " Example 3". Solve: x^2 - 23x + 102 = 0. Both roots are positive. Compose factor pairs of c = 102 with all positive numbers. Proceeding: (1, 102)(2, 51)(3, 34)(6, 17). This last sum is: 17 + 6 = 23 = -b. The 2 real roots are: 6 and 17.
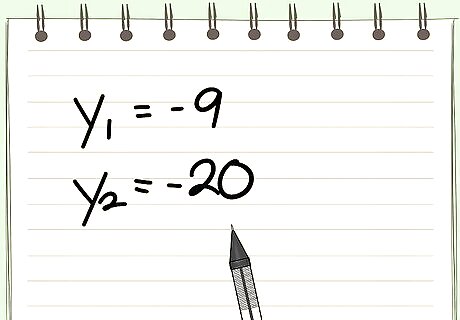
Assume that the 2 real roots of the simplified equation (2) are: y1, and y2.
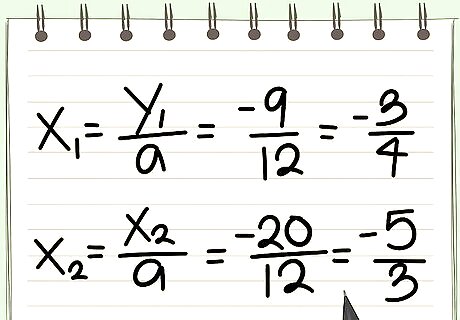
Divide both real roots y1 and y2 by the coefficient a to get the 2 real roots x1, and x2 of the original equation (1). Examples of solving by the new "Transforming Method" Example 3. Original equation to solve: 6x^2 - 19x - 11 = 0. (1). First, solve the transformed equation: x^2 - 19x - 66 = 0.(2). Roots have different signs. Compose factor pairs of a*c = -66. Proceeding: (-1, 66)(-2, 33)(-3, 22). This last sum is 22 - 3 = 19 = -b. Then, the 2 real roots of (2) is: y1 = -3, and y2 = 22. Next, divide both y1, and y2 by a = 6. The 2 real roots of the original equation (1) are: x1 = y1/6 = -3/6 = -1/2, and x2 = y2/6 = 22/6 = 11/3. Example 4. Original equation to solve: 6x^2 - 11x - 35 = 0 (1).
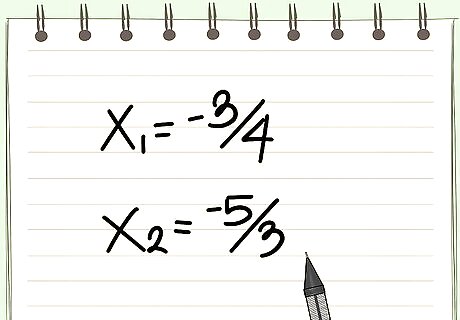
Solve the transformed equation: x^2 - 11x - 210 = 0 (2). Roots have different signs. To save time, compose factor pairs from the middle of the factor chain. Proceeding: .....(-5, 42)(-7, 30)(-10, 21). This last sum is: 21 - 10 = 11 = -b. Then, y1 = -10, and y2 = 21. Next, find the 2 real roots of the original equation (1): x1 = y1/6 = -10/6 = -5/3, and x2 = 21/6 = 7/2.. Example 5. Original equation: 12x^2 + 29x + 15 = 0. (1). Solve transformed equation: x^2 + 29x + 180 = 0 (2). Both roots are negative. Start composing a*c = 180 from the middle of the factor chain. Proceeding:..... (-5, -36)(-6, -30)(-9, -20). This last sum is: -29 = -b. The 2 real roots of (2) are: y1 = -9, and y2 = -20. Next, find the 2 real roots of (1): x1 = -9/12 = -3/4, and x2 = -20/12 = -5/3.




















Comments
0 comment