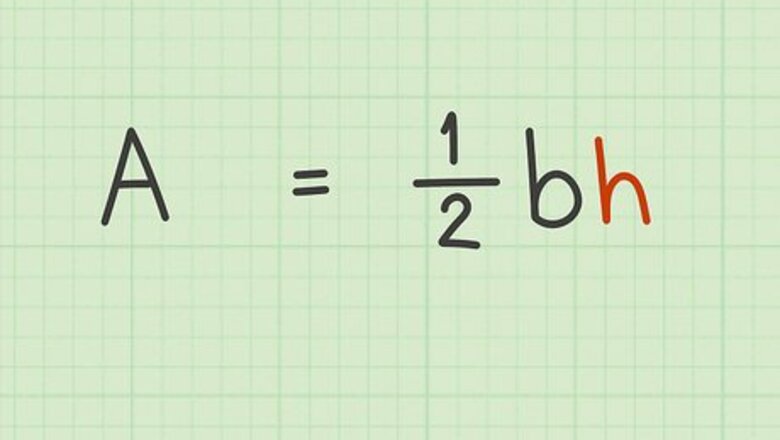
views
X
Research source
You will often need to do this when rearranging geometric formulas or when solving linear equations. In order to solve literal equations, use the same algebraic principles you would use to solve linear equations.
Rearranging Geometric Formulas
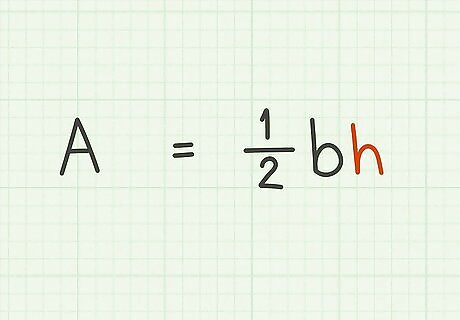
Determine which variable you need to isolate. Isolating a variable means getting the variable on one side of an equation by itself. This information should be given to you, or you can figure it out based on what information you know you will be given. For example, you might be told to solve the area of a triangle formula for h {\displaystyle h} h. Or, you might know that you have the area and base of the triangle, so you need to solve for the height. So, you need to rearrange the formula and isolate the h {\displaystyle h} h variable.
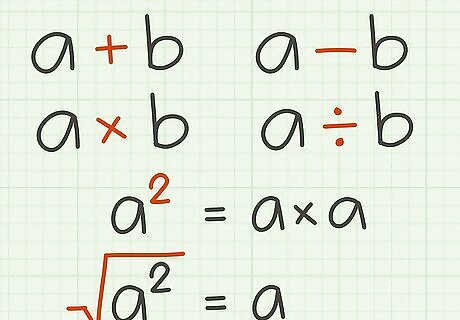
Use algebra to solve for the desired variable. Use inverse operations to cancel variables on one side of the equation and move them to the other side. Keep in mind the following inverse operations: Multiplication and division. Addition and subtraction. Squaring and taking a square root.

Keep the equation balanced. Whatever you do to one side of the equation, you must also do to the other side. This ensures that your equation remains true, and in the process you are moving variables from one side to the other as needed. For example, to solve the area of a triangle formula ( A = 1 2 b h {\displaystyle A={\frac {1}{2}}bh} A={\frac {1}{2}}bh) for h {\displaystyle h} h: Cancel the fraction by multiplying each side by 2: A × 2 = 2 × 1 2 b h {\displaystyle A\times 2=2\times {\frac {1}{2}}bh} A\times 2=2\times {\frac {1}{2}}bh 2 A = b h {\displaystyle 2A=bh} 2A=bh Isolate h {\displaystyle h} h by dividing each side by b {\displaystyle b} b: 2 A b = b h b {\displaystyle {\frac {2A}{b}}={\frac {bh}{b}}} {\frac {2A}{b}}={\frac {bh}{b}} 2 A b = h {\displaystyle {\frac {2A}{b}}=h} {\frac {2A}{b}}=h Rearrange the formula, if desired: h = 2 A b {\displaystyle h={\frac {2A}{b}}} h={\frac {2A}{b}}
Rearranging Equations of Lines
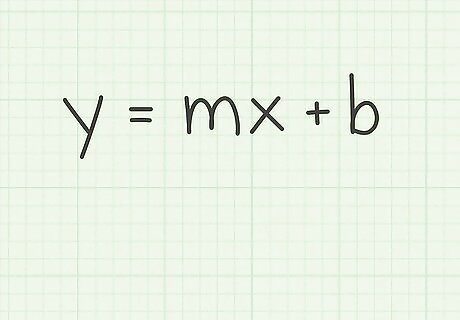
Remember the slope-intercept form for the equation of a line. The slope-intercept form is y = m x + b {\displaystyle y=mx+b} y=mx+b, where y {\displaystyle y} y equals the y-coordinate of a point on the line, x {\displaystyle x} x equals the x-coordinate of that same point, m {\displaystyle m} m equals the slope of the line, and b {\displaystyle b} b equals the y-intercept.
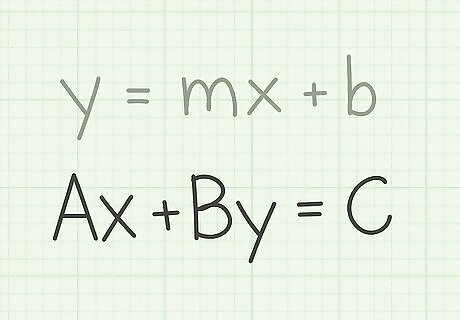
Remember the standard form of a line. The standard form is A x + B y = C {\displaystyle Ax+By=C} Ax+By=C, where x {\displaystyle x} x and y {\displaystyle y} y are the coordinates of a point on the line, A {\displaystyle A} A is a positive integer, and B {\displaystyle B} B and C {\displaystyle C} C are integers.
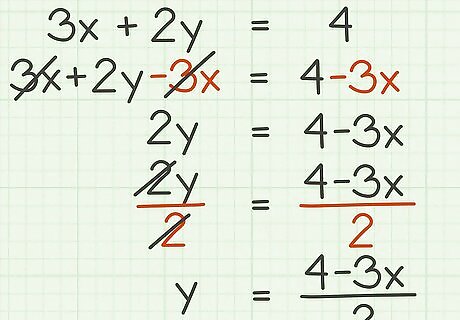
Use algebra to isolate the appropriate variable. Use inverse operations to move variables from one side of the equation to the other side. Remember to keep the equation balanced, which means that whatever you do to one side of the equation, you must also do to the other side. For example, you might have the equation of a line 3 x + 2 y = 4 {\displaystyle 3x+2y=4} 3x+2y=4. This is in standard form. If you need to find the y-intercept of the line, you need to rearrange the formula to slope-intercept form by isolating the y {\displaystyle y} y variable: Subtract 3 x {\displaystyle 3x} 3x from both sides of the equation: 3 x + 2 y − 3 x = 4 − 3 x {\displaystyle 3x+2y-3x=4-3x} 3x+2y-3x=4-3x 2 y = 4 − 3 x {\displaystyle 2y=4-3x} 2y=4-3x. Divide both sides by 2 {\displaystyle 2} 2: 2 y 2 = 4 − 3 x 2 {\displaystyle {\frac {2y}{2}}={\frac {4-3x}{2}}} {\frac {2y}{2}}={\frac {4-3x}{2}} y = 4 − 3 x 2 {\displaystyle y={\frac {4-3x}{2}}} y={\frac {4-3x}{2}} EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher To solve an equation for a variable like "x," you need to manipulate the equation to isolate x. Use techniques like the distributive property, combining like terms, factoring, adding or subtracting the same number, and multiplying or dividing by the same non-zero number to isolate "x" and find the answer.
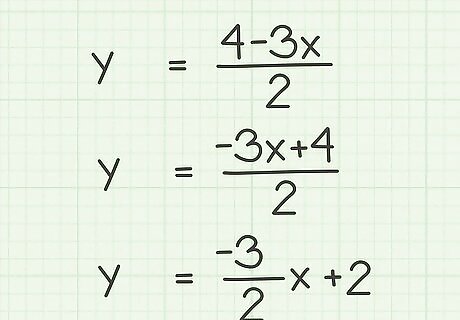
Reorder the variables and constants, if necessary. If you are changing an equation to slope-intercept or standard form, rearrange the variables, coefficients, and constants so that they follow the correct formula. For example, to change y = 4 − 3 x 2 {\displaystyle y={\frac {4-3x}{2}}} y={\frac {4-3x}{2}} to the correct slope-intercept formula, you need to switch the order of the number in the numerator, then simplify: y = − 3 x + 4 2 {\displaystyle y={\frac {-3x+4}{2}}} y={\frac {-3x+4}{2}} y = − 3 2 x + 2 {\displaystyle y={\frac {-3}{2}}x+2} y={\frac {-3}{2}}x+2Now, since the formula is in proper slope-intercept form, it is easy to identify the y-intercept as 2.
Solving Sample Problems
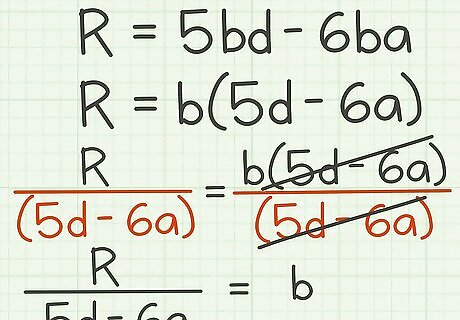
Solve this equation for b {\displaystyle b} b. R = 5 b d − 6 b a {\displaystyle R=5bd-6ba} R=5bd-6ba. Factor out the b {\displaystyle b} b: R = b ( 5 d − 6 a ) {\displaystyle R=b(5d-6a)} R=b(5d-6a). Isolate the b {\displaystyle b} b by dividing each side by the expression in parentheses: R 5 d − 6 a = b ( 5 d − 6 a ) 5 d − 6 a {\displaystyle {\frac {R}{5d-6a}}={\frac {b(5d-6a)}{5d-6a}}} {\frac {R}{5d-6a}}={\frac {b(5d-6a)}{5d-6a}} R 5 d − 6 a = b {\displaystyle {\frac {R}{5d-6a}}=b} {\frac {R}{5d-6a}}=b
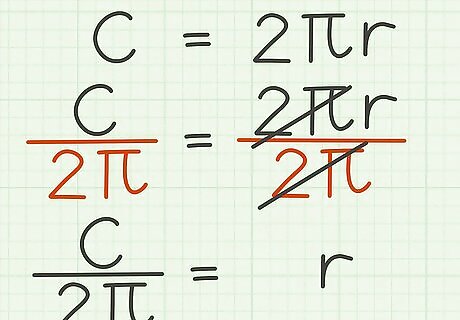
Solve the circumference of a circle formula for the radius. The formula is C = 2 π r {\displaystyle C=2\pi {r}} C=2\pi {r} Understand what each variable stands for. In this formula, C {\displaystyle C} C is the circumference, and r {\displaystyle r} r is the radius. So you need to isolate the r {\displaystyle r} r to solve for the radius. Isolate the r {\displaystyle r} r by dividing both sides of the equation by 2 π {\displaystyle 2\pi } 2\pi : C 2 π = 2 π r 2 π {\displaystyle {\frac {C}{2\pi }}={\frac {2\pi {r}}{2\pi }}} {\frac {C}{2\pi }}={\frac {2\pi {r}}{2\pi }} C 2 π = r {\displaystyle {\frac {C}{2\pi }}=r} {\frac {C}{2\pi }}=r If desired, reverse the order of the equation for standard form: r = C 2 π {\displaystyle r={\frac {C}{2\pi }}} r={\frac {C}{2\pi }}.
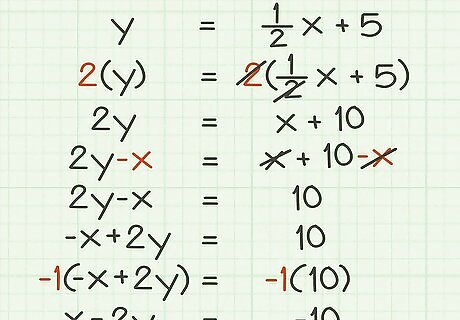
Rewrite this equation of a line in standard form. y = 1 2 x + 5 {\displaystyle y={\frac {1}{2}}x+5} y={\frac {1}{2}}x+5 Recall that standard form is A x + B y = C {\displaystyle Ax+By=C} Ax+By=C. Cancel the fraction by multiplying each side of the equation by 2: 2 y = 2 ( 1 2 x + 5 ) {\displaystyle 2y=2({\frac {1}{2}}x+5)} 2y=2({\frac {1}{2}}x+5) 2 y = x + 10 {\displaystyle 2y=x+10} 2y=x+10 Subtract x {\displaystyle x} x from both sides of the equation: 2 y − x = x + 10 − x {\displaystyle 2y-x=x+10-x} 2y-x=x+10-x 2 y − x = 10 {\displaystyle 2y-x=10} 2y-x=10 Rearrange the y {\displaystyle y} y and x {\displaystyle x} x variables so that they are in the standard form: − x + 2 y = 10 {\displaystyle -x+2y=10} -x+2y=10. Multiply both sides by − 1 {\displaystyle -1} -1, since A {\displaystyle A} A should be a positive integer for standard form: − 1 ( − x + 2 y ) = − 1 ( 10 ) {\displaystyle -1(-x+2y)=-1(10)} -1(-x+2y)=-1(10) x − 2 y = − 10 {\displaystyle x-2y=-10} x-2y=-10


















Comments
0 comment