views
- To estimate the tangent slope at a point, draw a tangent line at the point. Then, choose two points on the tangent line.
- Use the formula slope = (y2 - y1) / (x2 - x1) to find the tangent slope.
- To find the derivative, use the equation f’(x) = [f(x + dx) – f(x)] / dx, replacing f(x + dx) and f(x) with your given function.
- Simplify the equation and solve for dx→0. Replace dx in the equation with 0. This will give you the final derivative equation.
Estimate without an Equation
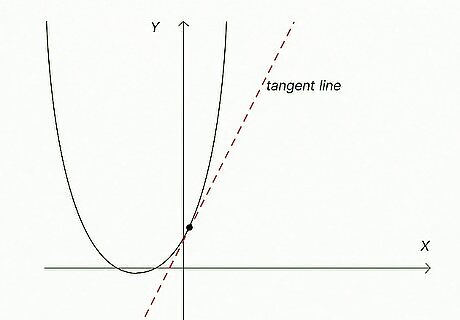
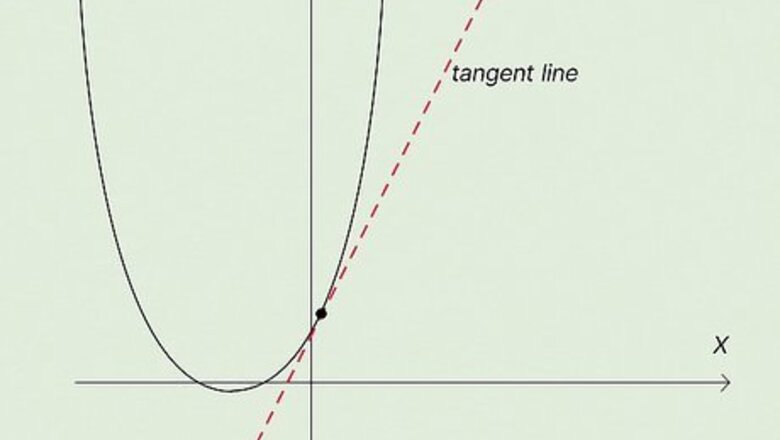
Draw a tangent line. Use a straightedge to draw a tangent line at the point on the graph that you want to estimate the derivative for. The derivative describes how the slope of a curve changes as x, the horizontal value, changes. Drawing a tangent line allows you to estimate the derivative (the tangent slope) at a given point. A tangent line is a straight line that touches a curve at a single point. The tangent slope is the slope of the tangent line. Make sure your curve and tangent line are drawn on a graph with grid lines. This will make it easier to calculate the tangent slope. Since this is a hand-drawn method, this calculation will only be an estimate, not the exact derivative at a point.
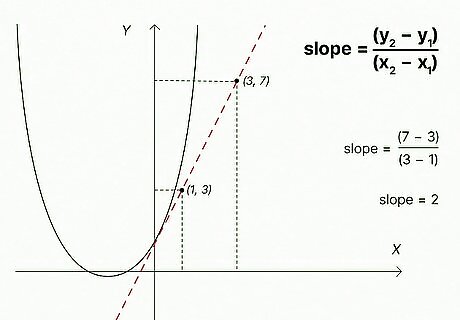
Find the slope of the tangent line. Choose two points that the tangent line passes through. Use the grid to find two simple points, preferably integers. The equation to find the slope with two points is slope = (y2 - y1) / (x2 - x1) using the points (x1, y1) and (x2, y2) for example, if you have the points (1, 3) and (3, 7), slope = (7 - 3) / (3 - 1) slope = 4 / 2 slope = 2
Finding the Derivative Equation

Review the formal definition of a derivative. The derivative can be defined as the equation: (df / dx)(x) = [f(x + dx) – f(x)] / dx which can be written as f’(x) = [f(x + dx) – f(x)] / dx where f(x) is the function f of x (sometimes written as “y”), i.e. how the value of y changes as the value of x changes f’(x) is the derivative of f(x), as indicated by the prime symbol (’) dx is a small change in x that approaches 0 f(x + dx) is the value of y at the horizontal value x + dx
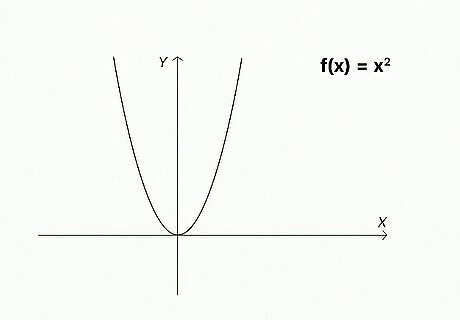
Identify the graph’s function. This will be f(x), the function for the curve on the graph. For example, f(x) = x^2. For more general calculus tips, see our guide on how to do well in calculus. If you’re looking for how to use derivative rules, check out How to Differentiate Polynomials.
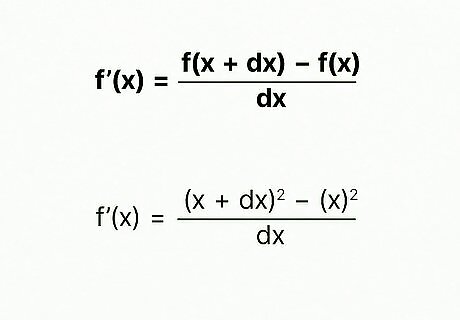
Write the formal definition using the given function. Replace the terms f(x + dx) and f(x) with your given function. For example, if you were given f(x) = x^2, you would write the formal definition as f’(x) = [(x + dx)^2 – (x)^2] / dx
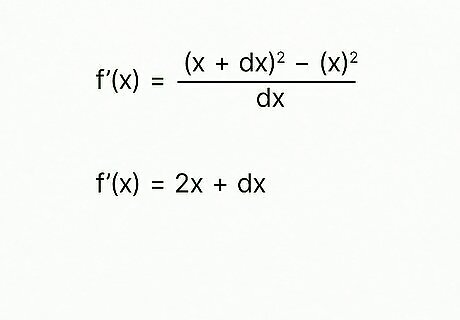
Simplify the equation. For simple functions, you can simplify the function algebraically. Here’s a step by step example for f’(x) = [(x + dx)^2 – (x)^2] / dx Our starting equation: f’(x) = [(x + dx)^2 – (x)^2] / dx Writing out the expanded polynomial term: f’(x) = [x^2 + 2xdx + dx^2 – x^2] / dx The terms x^2 and – x^2 equal zero, resulting in: f’(x) = [2xdx + dx^2] / dx Both terms in the numerator have a dx, which can cancel out with the dx in the denominator, giving the simplified equation: f’(x) = 2x + dx

Resolve the equation for dx→0. Replace every instance of dx with a 0. For our example, this would yield the equation: f’(x) = 2x + 0 which simplifies to: f’(x) = 2x So, the derivative of f(x) = x^2 is f’(x) = 2x
Finding the Tangent Slope at a Single Point
Find the derivative of the curve. Follow the previous method, Finding the Derivative Equation, to get the derivative equation for the given function f(x).
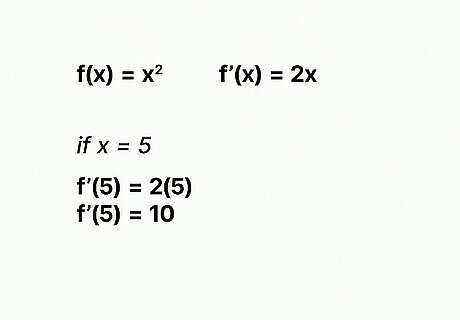
Insert the x value of the point. Replace x in the derivative function f’(x). Using our previous example: Find the slope of the tangent line at x = 5 for the function f(x) = x^2. f’(x) = 2x f’(5) = 2(5) f’(5) = 10 The slope of the tangent line at x = 5 is 10.


















Comments
0 comment