Using the Empirical Rule to Analyze Data and Draw Conclusions

Setting Up Your Curve

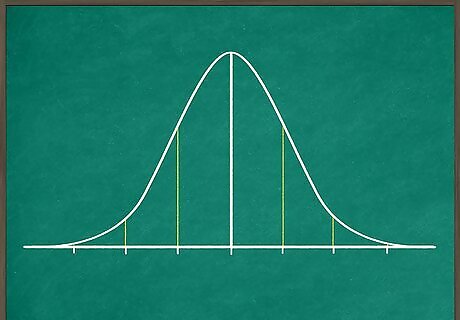
Draw out and divide a bell curve. Sketch out a normal curve, where the highest point is in the middle, and the ends slope down and taper off symmetrically to the left and right. Next, draw several vertical lines intersecting the curve: 1 line should divide the curve in half. Draw 3 lines to the right of this middle line, and 3 more to the left. These should divide each of the curve's halves into 3 evenly spaced sections and one tiny section at the tip.

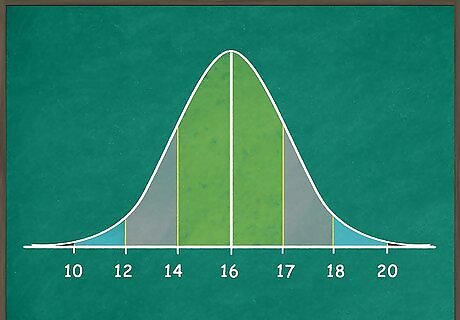
Write the values from your normal distribution on the dividing lines. Mark the line in the middle with the mean of your data. Then, add standard deviations to get the values for the 3 lines to the right. Subtract standard deviations from your mean to get values for the 3 lines to the left. For example: Suppose your data has a mean of 16 and a standard deviation of 2. Mark the center line with. 16. Add standard deviations to mark the first line to the right of the center with 18, the next to the right with 20, and the rightmost line with 22. Subtract standard deviations to mark the first line to the left of the center with 14, the next line to the left with 12, and the leftmost line with 10.

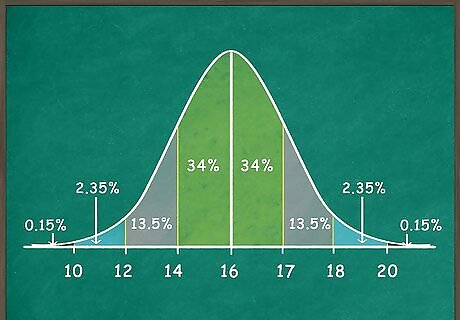
Mark the percentages for each section. The basic point empirical rule is easy to grasp: 68 percent of data points for a normal distribution will fall within 1 standard deviation of the mean, 95 percent within 2 standard deviations, and 99.7 percent within 3 standard deviations. To remind yourself, mark each section with a percentage: Each section immediately to the right and left of the center line will contain 34%, for a total of 68. The next sections to the right and left will each contain 13.5%. Add these to the 68 percent to get 95% of your data. The next sections over on each side will each contain 2.35% of your data. Add these to the 95 percent to get 99.7% of your data. The remaining tiny left and right tips of the data each contain 0.15% of the remaining data, for a total of 100%.

Solving Problems Using Your Curve

Find the distributions of your data. Take your mean, and use the empirical rule to find the distributions of data 1, 2, and 3 standard deviations from the mean. Write these on your curve for reference. For example, imagine you are analyzing the weights of a population of cats, where the mean weight is 4 kilograms, with a standard deviation of 0.5 kilograms: 1 standard deviation above the mean would equal 4.5 kg, and 1 standard deviation below equals 3.5 kg. 2 standard deviations above the mean would equal 5 kg, and 2 standard deviations below would equal 3 kg. 3 standard deviations above the mean would equal kg, and 3 standard deviations below would equal 2.5 kg.

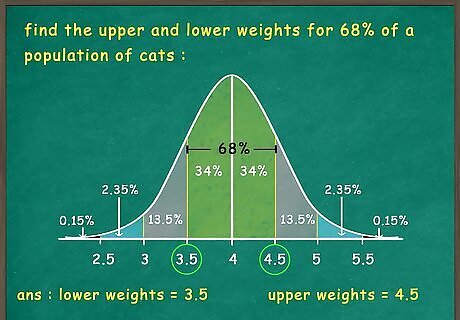
Determine the section of the curve your question asks you to analyze. Once you have your curve set up, you can use the Empirical Rule and simple arithmetic to solve data analysis questions. Start by reading your question carefully to figure out the sections you need to work with. For example: Imagine you are asked to find the upper and lower weights for 68% of a population of cats. You would need to look at the two centermost sections, where 68% of data will fall. Similarly, imagine the mean weight is 4 kilograms, with a standard deviation of 0.5 kilograms. If you are asked to find the proportion of cats above 5 kilograms, you need to look at the rightmost section (2 standard deviations away from the mean).

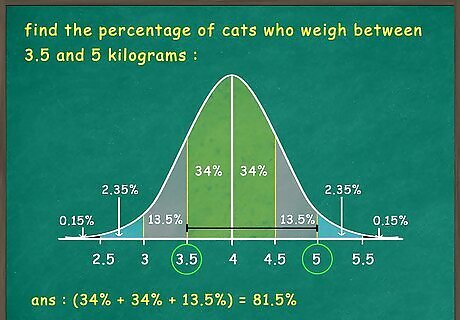
Find the percentage of your data within a certain range. If you’re asked to find the percentage of the population between a certain range, all you have to do is add up the percentages within a given set of standard deviations. For instance, if you are asked to find the percentage of cats who weigh between 3.5 and 5 kilograms, if the mean weight is 4 kilograms, with a standard deviation of 0.5 kilograms: 2 standard deviations above the mean will be 5 kilograms, and 1 standard deviation below the mean will be 3.5 kilograms. This means that 81.5% (68% + 13.5%) of the cats weigh between 3.5 and 5 kilograms.

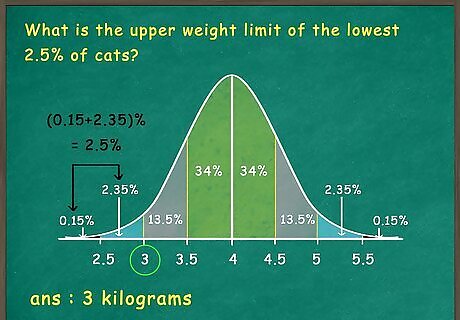
Use the section percentages to find data points and ranges. Take the information provided by the percentage distributions and standard deviations to find upper and lower limits for portions of your data. For instance, a question about your cat weight data may ask: “What is the upper weight limit of the lowest 2.5% of cats?” The lowest 2.5% of data would fall below 2 standard deviations from the mean. If the mean is 4 kilograms, and standard deviation is 0.5, then the lowest 2.5% of cats will weight 3 kilograms or less (4 - 0.5 x 2).