views
For this method, you will need to know how to convert numbers into binary form. If you don't know how to do this, you can learn how in How to Convert from Decimal to Binary.
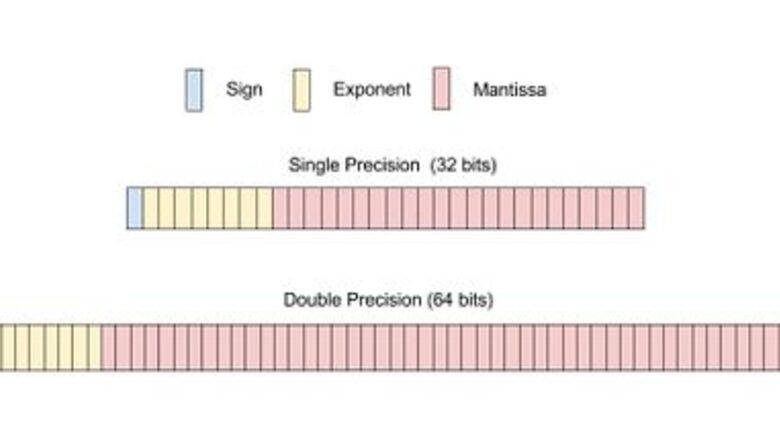
Choose single or double precision. When writing a number in single or double precision, the steps to a successful conversion will be the same for both, the only change occurs when converting the exponent and mantissa. First we must understand what single precision means. In floating point representation, each number (0 or 1) is considered a “bit”. Therefore single precision has 32 bits total that are divided into 3 different subjects. These subjects consist of a sign (1 bit), an exponent (8 bits), and a mantissa or fraction (23 bits). Double precision, on the other hand, has the same setup and same 3 parts as single precision; the only difference is that it will be larger and more precise number. In this case, the sign will have 1 bit, the exponent will have 11 bits and the mantissa will have 52 bits. In this example will convert the number 85.125 into IEEE 754 single precision.

Separate the whole and the decimal part of the number. Take the number that you would like to convert, and take apart the number so you have a whole number portion and a decimal number portion. This example will use the number 85.125. You can separate that into whole number 85, and the decimal 0.125.
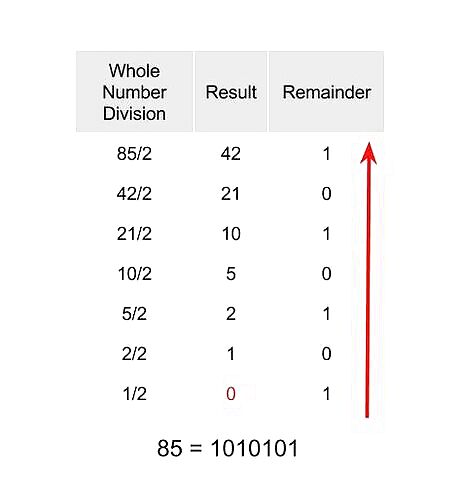
Convert the whole number into binary. This would be the 85 from 85.125, which will be 1010101 when converted into binary.
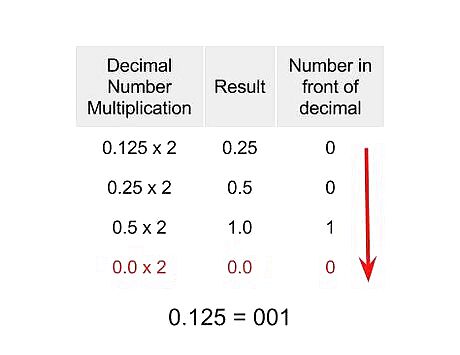
Convert the decimal portion into binary. This would be the 0.125 from 85.125, which will be 0.001 when converted into binary.
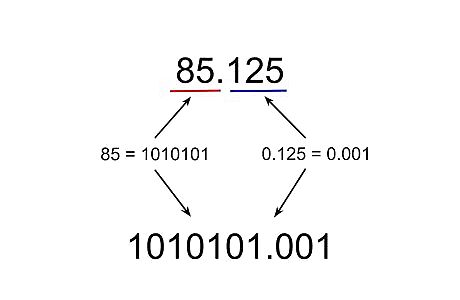
Combine the two parts of the number that have been converted into binary. For instance, the number 85 in binary is 1010101 and the decimal portion 0.125 in binary is .001. When you combine them using a decimal point, you end up with 1010101.001 as your final answer.
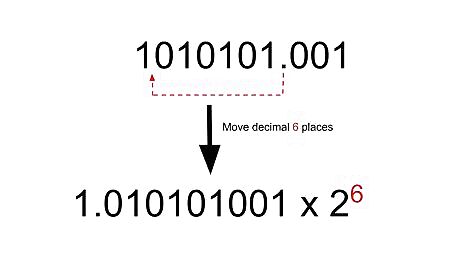
Convert the binary number into base 2 scientific notation. You can convert the number into base 2 scientific notation by moving the decimal point over to the left until it is to the right of the first bit. These numbers are normalized which means the leading bit will always be 1. As for the exponent, the number of times that you moved the decimal will be your exponent in base 2 scientific notation. Remember that moving the decimal to the left will result in a positive exponent while moving the decimal to the right will result in a negative exponent. For our example, you will need to move the decimal 6 times in order to get it to the right of the first bit. The resulting notation will be 01.010101001 ∗ 2 6 {\displaystyle 01.010101001*2^{6}} 01.010101001*2^{6} , this number will be used in future steps.
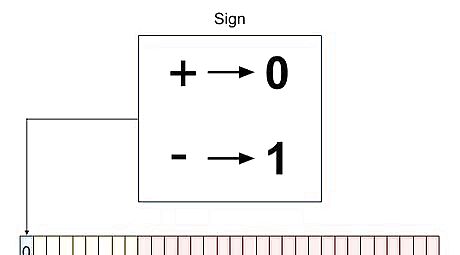
Determine the sign of the number and display in binary format. You will now determine if your original number is positive or negative. If the number is positive, you will record that bit as 0, and if it is negative, you will record that bit as 1. Since your original number, 85.125, is positive, you will record that bit as 0. This will be the first bit out of the 32 total bits in your IEEE 754 single precision representation.

Get the exponent based on precision. There are set biases for both single and double precision. The exponent bias for single precision is 127, which means we must add the base 2 exponent found previously to it. Thus, the exponent you will use is 127+6 which is 133. Double precision as perceived from the name is more precise and can hold larger numbers. Therefore its exponent bias is 1023. The same steps used for single precision apply here, so the exponent you can use to find double precision is 1029.

Turn the exponent into binary. After you determine your final exponent, you will need to convert it into binary so that it could be used in the IEEE 754 conversion. For the example, you can convert the 133 that you found in the last step into 10000101.
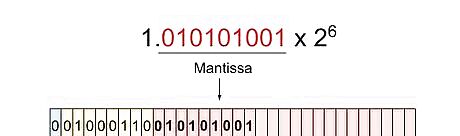
Determine the mantissa. The mantissa aspect, or the third part of the IEEE 754 conversion, is the rest of the number after the decimal of the base 2 scientific notation. You will just drop the 1 in the front and copy the decimal portion of the number that is being multiplied by 2. No binary conversion needed! For the example, the mantissa would be 010101001 from 01.010101001 ∗ 2 6 {\displaystyle 01.010101001*2^{6}} 01.010101001*2^{6}.

Compile 3 parts into one final number. Finally, you will compile all that we have calculated thus far into your conversion. It will first begin with a 0 or 1 bit that you determined in step 7 based on sign. For the example, you will have a 0 to start it. Next up, you will have the exponent section that you determined in step 9. For the example, your exponent will be 10000101. Now, you have the mantissa, which is the third and last part of the conversion. You derived this earlier when you took the decimal portion of the base 2 conversion. For the example, the mantissa would be 010101001. Finally, you combine these all together. The order should go sign-exponent-mantissa. After you connect those three binary numbers, you then fill out the rest of the mantissa with 0s. For the example the solution is 0 10000101 01010100100000000000000 as 85.125 converted into IEEE 754 format.
















Comments
0 comment