views
Calculating Porosity Theoretically by Volumes
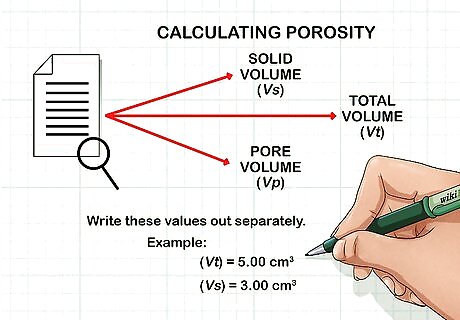
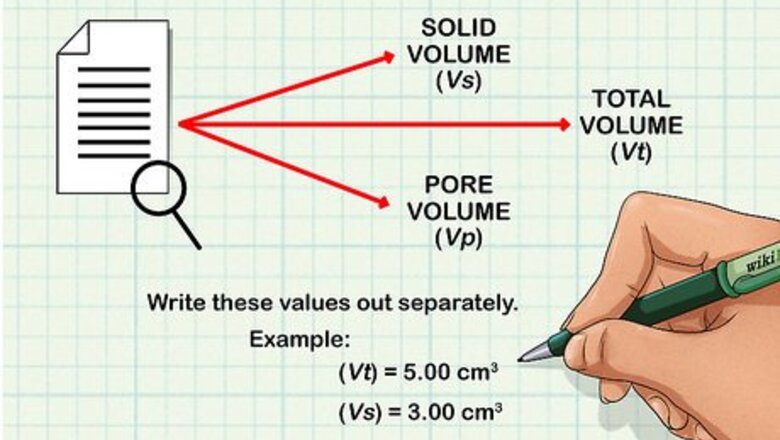
Extract useful values from the given information. When calculating porosity theoretically, you will be given an example situation that contains some of the values you need. Read your question carefully and look for values such as total volume ( V t {\displaystyle Vt} Vt), solid volume ( V s {\displaystyle Vs} Vs), and pore volume ( V p {\displaystyle Vp} Vp). Always pay close attention to the units of these values. It will help to write these values out separately. For example, if your question provides V t {\displaystyle Vt} Vt and V s {\displaystyle Vs} Vs, you would write: V t {\displaystyle Vt} Vt = 5.00 cm^3 V s {\displaystyle Vs} Vs = 3.00 cm^3
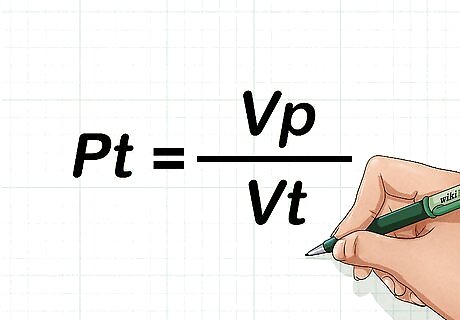
Set up the appropriate equation. By definition, porosity ( P t {\displaystyle Pt} Pt) is equal to the pore volume ( V p {\displaystyle Vp} Vp) divided by the total volume ( V t {\displaystyle Vt} Vt), or P t {\displaystyle Pt} Pt = V p {\displaystyle Vp} Vp/ V t {\displaystyle Vt} Vt. Keep in mind that this is not the only equation that can find porosity. If values are given for bulk density and particle density rather than values for volumes, you should use a different equation.
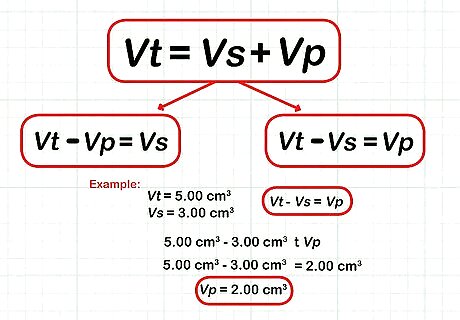
Find values for your volume variables. It is helpful to keep in mind that V t {\displaystyle Vt} Vt is the sum of solid and pore volumes, or V t {\displaystyle Vt} Vt = V s {\displaystyle Vs} Vs + V p {\displaystyle Vp} Vp. This relationship can be rearranged to allow you to solve for the any of the volume variables, as long as the other two are known. For example, and V t {\displaystyle Vt} Vt - V p {\displaystyle Vp} Vp = V s {\displaystyle Vs} Vs. Using the same values as listed in previous steps, V t {\displaystyle Vt} Vt = 5.00 cm^3 and V s {\displaystyle Vs} Vs = 3.00 cm^3, we can solve V t {\displaystyle Vt} Vt - V s {\displaystyle Vs} Vs = V p {\displaystyle Vp} Vp to find that V p {\displaystyle Vp} Vp = 5.00 cm^3 - 3.00 cm^3 = 2.00 cm^3.

Plug your known volume variables into the porosity equation. Once you have determined a value for V p {\displaystyle Vp} Vp and a value for V t {\displaystyle Vt} Vt, you can plug them into the porosity equation, P t {\displaystyle Pt} Pt = V p {\displaystyle Vp} Vp/ V t {\displaystyle Vt} Vt. Be sure that you include units for V p {\displaystyle Vp} Vp and V t {\displaystyle Vt} Vt. Also, you should be sure that the units match, if not, you will need to do dimensional analysis to make them match. It’s important to match the units because porosity is a unitless value that is usually expressed as a percentage. The units from the volume variables will cancel each other out by division.

Solve the equation to obtain a porosity value. Now that your equation is totally set up and has the appropriate values in place, you can solve by doing simple arithmetic. It might help to have a calculator handy for this part. Since porosity is often expressed as a percent, once you have found the decimal value, it is common to multiply this value by 100%. Using the same values from the above examples, your equation will look similar to this: P t {\displaystyle Pt} Pt = 2.00 cm^3 / 5.00 cm^3 = 0.400. If you would like to express that value as a percent, you would multiply it by 100% to yield P t {\displaystyle Pt} Pt = 40%.
Calculating Porosity Theoretically by Densities

Assume the particle density ( P d {\displaystyle Pd} Pd) of your sample to be 2.66 g/(cm^3). The particle density of a sample is equal to the mass of the sample divided by volume of the sample. When dealing with soil samples, the average particle density of soil is 2.66 g/(cm^3). For that reason, this value is assumed to be the particle density of any soil sample, unless otherwise specified.
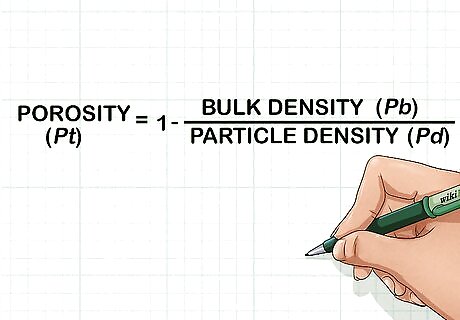
Use the relationship between volume and density to derive your equation. Since density is defined as mass per volume, and porosity is a comparison of pore volume to total volume, it is possible to express porosity in terms of density as well. The result is the equation P t {\displaystyle Pt} Pt = (1 - P b {\displaystyle Pb} Pb/ P d {\displaystyle Pd} Pd) where P t {\displaystyle Pt} Pt is your porosity, P b {\displaystyle Pb} Pb is the bulk density, and P d {\displaystyle Pd} Pd is the sample’s particle density.
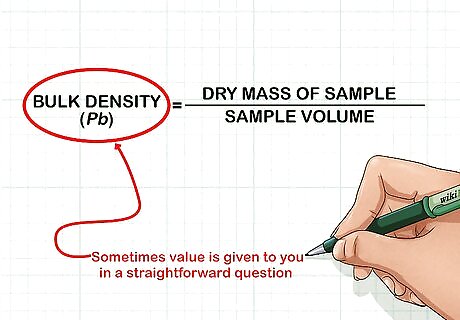
Find your P b {\displaystyle Pb} Pb value. The P b {\displaystyle Pb} Pb value will be given to you in a straightforward question. If the value is not given, you may be given other values such as the dry mass of the sample and the sample’s volume. In this case you would divide the dry mass of the sample by the sample volume to find your bulk density, or P b {\displaystyle Pb} Pb.

Solve the equation by inserting the appropriate density values. Now that you have obtained values for P b {\displaystyle Pb} Pb and P d {\displaystyle Pd} Pd, you can solve for P t {\displaystyle Pt} Pt. Note that the value obtained by dividing P b {\displaystyle Pb} Pb by P d {\displaystyle Pd} Pd should ALWAYS be less than 1, thus the equation P t {\displaystyle Pt} Pt = (1 - P b {\displaystyle Pb} Pb/ P d {\displaystyle Pd} Pd) should never yield a negative answer. If it does, you likely divided P d {\displaystyle Pd} Pd by P b {\displaystyle Pb} Pb, which is incorrect. This equation will give you a decimal value for porosity. To express porosity as a percent, simply multiply that decimal by 100%. For example, 0.41 x 100% = 41%.
Calculating Porosity Experimentally by Saturation

Measure the volume of your sample. You can measure the volume directly if your sample exactly fills a container with a known volume. You can also transfer the sample to a container such as a pre-measured beaker to measure volume. If you are unable to measure the volume directly, you can calculate the volume mathematically. Note that transferring the sample from one container to another may affect the porosity by disrupting the material.

Measure a volume of water. It is not important exactly how much water you measure out. The two things that are important in this step are measuring out more water than you will need to saturate your sample, and writing down exactly how much water you started with. This is the only way you can know how much you used.

Saturate the sample with water. This is an easy step, but can tricky. You want to add enough water so that all of the pores in your sample are filled, but you do not want to add any extra water. While it is important to get as close as you can to exactly saturating the sample, there will be some degree of error. Get the water level as close to the surface level of your solid sample level as possible.
Record the volume of water used. To do this, you will need to subtract the volume of water that is left from the volume of water you started with. This will leave you with the volume of water that was poured out. The volume of water you used is (approximately) equal to the pore volume of your sample.
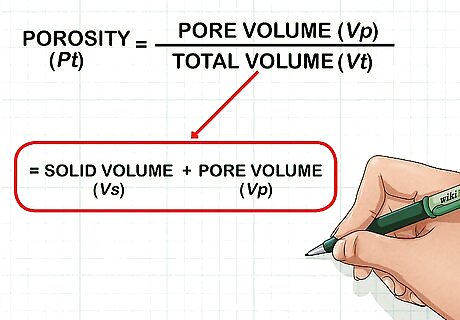
Set up the equation to solve for porosity with volume. Now that you have the volume of your sample ( V s {\displaystyle Vs} Vs) and the pore volume ( V p {\displaystyle Vp} Vp), you can add them together to get total volume ( V t {\displaystyle Vt} Vt). It is now possible to use the equation P t {\displaystyle Pt} Pt = ( V p {\displaystyle Vp} Vp/ V t {\displaystyle Vt} Vt) x 100% to find your porosity ( P t {\displaystyle Pt} Pt).

Do the calculations to find your sample’s porosity. Enter the appropriate values into the equation. Be sure to keep track of your units and make sure that they cancel out appropriately, as porosity is a unitless value. A calculator might be handy for this step, also.
Calculating Porosity in the Field by Taking Core Samples

Saturate the area you want to sample. A good way to do this is to place a pre-weighed steel ring (such as one with a diameter of 7 centimetres (2.8 in) and a height of 10 centimetres (3.9 in)) on the ground where you would like to take a sample and fill it with water. Allow the water to sit in the ring overnight, or until it is absorbed by the ground. This will make it easier to collect your sample. You can find pre-weighed steel rings in home improvement stores and online.
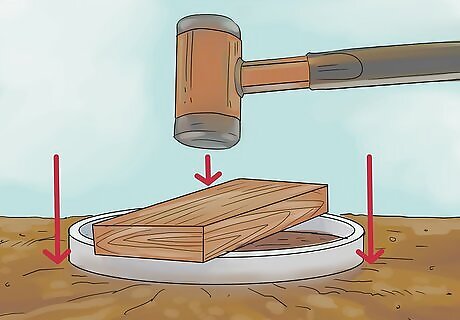
Drive the steel ring into the ground. Use a block of wood and a hammer to drive the ring down into the ground. The soil inside the ring is referred to as a core or core sample. The ring protects the core sample from being disturbed during collection.
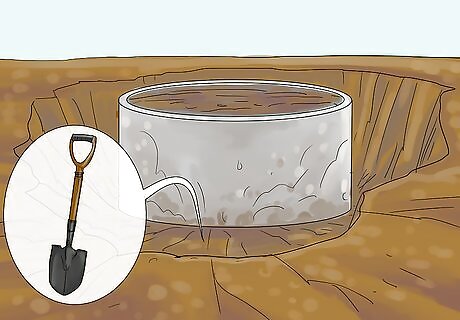
Dig out around the steel ring. Use a spade and other digging tools to carefully dig around the steel ring. You do not want to disturb the soil inside the ring. Cut away any roots from the bottom of the ring.

Remove the ring. Once you have cleared out the soil around the ring, you can remove the ring and sample from the hole. Keep the core sample inside the ring and do not disturb it. Be careful not to lose any of the sample when moving it.
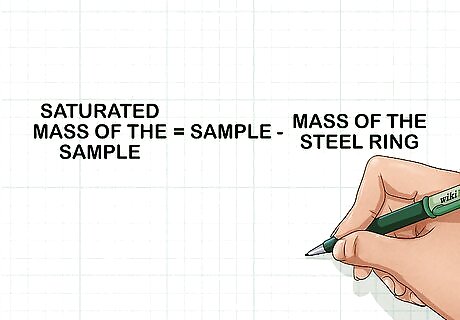
Record the saturated mass of your sample. Put the ring in a large, clear container. Add water until the sample in the ring is fully saturated and can hold no more water. Weigh the sample in the steel ring. Subtract from that value the mass of the steel ring. This will leave you with the saturated mass of your sample.
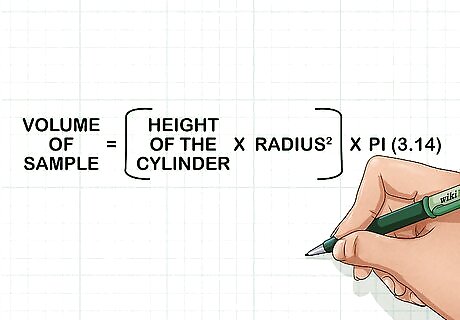
Record the volume of your sample. The volume of your sample will be the same as the volume of your ring. Since your ring is a cylinder, to calculate the volume you will multiply the height of the cylinder by the radius squared (the radius is the distance from the center of the circle to the edge), and then multiply that by pi (often rounded to 3.14). If you do not know the radius you can measure across the top of the cylinder at its widest point and divide that measurement by two.

Transfer the soil to an oven safe container. Be sure to pre-weigh the container and write down the mass of the container ( m c {\displaystyle mc} mc). If you are planning to use a microwave oven to dry your sample, be sure that your container has no metal and is microwave safe.
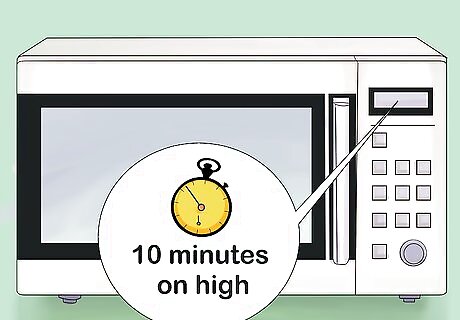
Dry your sample. If you are using a microwave, 10 minutes on high should be sufficient to dry out your sample. This ensures that all of the pores in the sample have been cleared of water. You can also dry the sample in a conventional oven at a temperature of 105 degrees Celsius, or 221 degrees Fahrenheit, for at least 2 hours.Though they are still full of air, this will not affect the mass of the sample.
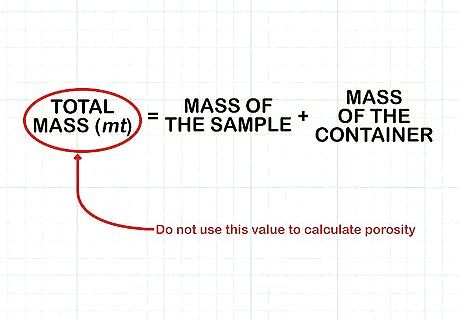
Weigh your dried sample in the dish to find your total mass ( m t {\displaystyle mt} mt). Remember that this value is not the mass of your sample. It is the mass of your sample plus the mass of your container. Do not use this value to calculate porosity.
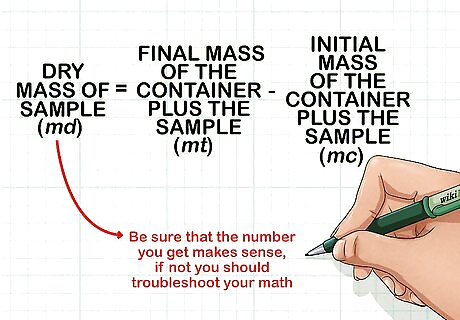
Subtract m c {\displaystyle mc} mc from m t {\displaystyle mt} mt to find the dry mass of your sample ( m d {\displaystyle md} md). To find the dry weight of your sample, you can simply subtract the initial mass of the container from the final mass of the container plus the sample. Be sure that the number you get makes sense. For example, you will not have a negative value for mass. If you do, this is incorrect and you should troubleshoot your math.

Calculate the mass of water in the saturated sample. Subtract the dry mass ( m d {\displaystyle md} md) from the saturated mass ( m s {\displaystyle ms} ms). The difference will be the mass of water ( m w {\displaystyle mw} mw). Again, the dry mass should be smaller than the saturated mass.

Convert the mass of water to the pore volume of your sample. By definition, one gram of water is equal to one cubic centimeter of water. This means that the mass of your water in grams is equal to the volume of water in cubic centimeters. Since your sample was saturated, all pores are filled with water, therefore, the pore volume is equal to the volume of water present in the saturated sample.

Divide the pore volume by the total volume of your sample. This will yield a decimal number that is smaller than one. Multiply that number by 100%. The result is the porosity of your sample expressed as a percent.


















Comments
0 comment