
views
Dividing a Fraction by a Fraction
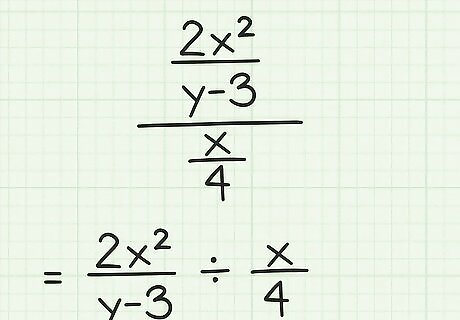
Rewrite the complex fraction as a division problem. Remember that a fraction bar means “divided by,” so when you see a fraction over a fraction, you need to divide the top fraction by the bottom fraction. For example, you might see 2 x 2 y − 3 x 4 {\displaystyle {\frac {\frac {2x^{2}}{y-3}}{\frac {x}{4}}}} {\frac {{\frac {2x^{{2}}}{y-3}}}{{\frac {x}{4}}}}. You can rewrite this as 2 x 2 y − 3 ÷ x 4 {\displaystyle {\frac {2x^{2}}{y-3}}\div {\frac {x}{4}}} {\frac {2x^{{2}}}{y-3}}\div {\frac {x}{4}}.
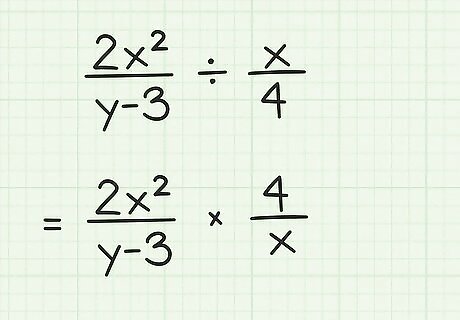
Take the reciprocal of the second fraction. To divide a fraction by a fraction, you take the reciprocal of the second fraction, and you change the division sign to a multiplication sign. A reciprocal is a fraction in which the numerator and denominator are reversed. For example: 2 x 2 y − 3 ÷ x 4 {\displaystyle {\frac {2x^{2}}{y-3}}\div {\frac {x}{4}}} {\frac {2x^{{2}}}{y-3}}\div {\frac {x}{4}}becomes 2 x 2 y − 3 × 4 x {\displaystyle {\frac {2x^{2}}{y-3}}\times {\frac {4}{x}}} {\frac {2x^{{2}}}{y-3}}\times {\frac {4}{x}}
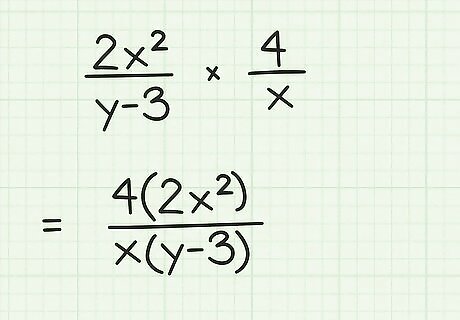
Rewrite the expression as a single fraction. Use parentheses to show the multiplication, but do not multiply any terms yet. Writing the expression this way may help you identify terms that can cancel. For example, 2 x 2 y − 3 × 4 x = 4 ( 2 x 2 ) x ( y − 3 ) {\displaystyle {\frac {2x^{2}}{y-3}}\times {\frac {4}{x}}={\frac {4(2x^{2})}{x(y-3)}}} {\frac {2x^{{2}}}{y-3}}\times {\frac {4}{x}}={\frac {4(2x^{{2}})}{x(y-3)}}.
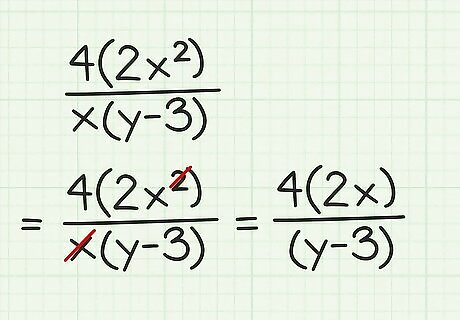
Simplify the expression. Use the normal rules for simplifying a rational expression to do this. Cancel out terms common to the numerator and denominator. Remember that you cannot cancel out a single term (like y {\displaystyle y} y) from a binomial (like y − 3 {\displaystyle y-3} y-3). Also remember that if you have an x 2 {\displaystyle x^{2}} x^{{2}} term in the numerator, and an x {\displaystyle x} x term in the denominator, you can cancel out one x {\displaystyle x} x, and the x {\displaystyle x} x in the denominator disappears, and the x 2 {\displaystyle x^{2}} x^{{2}} in the numerator becomes x {\displaystyle x} x. For example, you can cancel an x {\displaystyle x} x in the numerator and denominator in the expression 4 ( 2 x 2 ) x ( y − 3 ) {\displaystyle {\frac {4(2x^{2})}{x(y-3)}}} {\frac {4(2x^{{2}})}{x(y-3)}}: 4 ( 2 x 2 ) x ( y − 3 ) {\displaystyle {\frac {4(2x^{\cancel {2}})}{{\cancel {x}}(y-3)}}} {\frac {4(2x^{{{\cancel {2}}}})}{{\cancel {x}}(y-3)}} 4 ( 2 x ) y − 3 {\displaystyle {\frac {4(2x)}{y-3}}} {\frac {4(2x)}{y-3}}
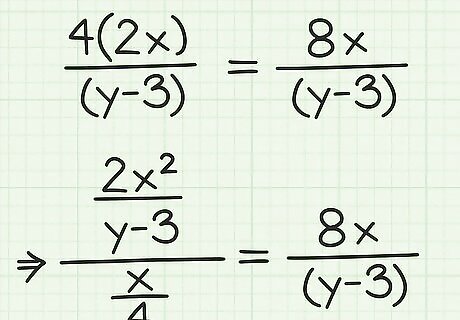
Complete the necessary multiplications. If you have any remaining parentheses in the numerator or denominator, simplify these by multiplying. The result will be your final simplified expression. For example, 4 ( 2 x ) y − 3 = 8 x y − 3 {\displaystyle {\frac {4(2x)}{y-3}}={\frac {8x}{y-3}}} {\frac {4(2x)}{y-3}}={\frac {8x}{y-3}}. So, 2 x 2 y − 3 x 4 = 4 ( 2 x ) y − 3 = 8 x y − 3 {\displaystyle {\frac {\frac {2x^{2}}{y-3}}{\frac {x}{4}}}={\frac {4(2x)}{y-3}}={\frac {8x}{y-3}}} {\frac {{\frac {2x^{{2}}}{y-3}}}{{\frac {x}{4}}}}={\frac {4(2x)}{y-3}}={\frac {8x}{y-3}}.
Applying Algebra Rules to Complex Problems
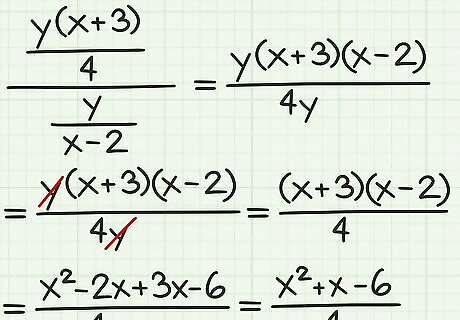
Use the FOIL method to multiply binomials. The FOIL method helps you remember to first multiply the first terms, then the outer terms, then the inner terms, then the last terms. When dividing a fraction by a fraction, this should be your last step after cancelling terms in the numerator and denominator. For example, if you are simplifying the expression y ( x + 3 ) 4 y x − 2 {\displaystyle {\frac {\frac {y(x+3)}{4}}{\frac {y}{x-2}}}} {\frac {{\frac {y(x+3)}{4}}}{{\frac {y}{x-2}}}}, after taking the reciprocal and combining terms, you end up with the expression y ( x + 3 ) ( x − 2 ) 4 y {\displaystyle {\frac {y(x+3)(x-2)}{4y}}} {\frac {y(x+3)(x-2)}{4y}}. First, cancel the y {\displaystyle y} y in the numerator and denominator, then multiply the binomials using the FOIL method: y ( x + 3 ) ( x − 2 ) 4 y {\displaystyle {\frac {{\cancel {y}}(x+3)(x-2)}{4{\cancel {y}}}}} {\frac {{\cancel {y}}(x+3)(x-2)}{4{\cancel {y}}}} ( x + 3 ) ( x − 2 ) 4 {\displaystyle {\frac {(x+3)(x-2)}{4}}} {\frac {(x+3)(x-2)}{4}} x 2 − 2 x + 3 x − 6 4 {\displaystyle {\frac {x^{2}-2x+3x-6}{4}}} {\frac {x^{{2}}-2x+3x-6}{4}} x 2 + x − 6 4 {\displaystyle {\frac {x^{2}+x-6}{4}}} {\frac {x^{{2}}+x-6}{4}}
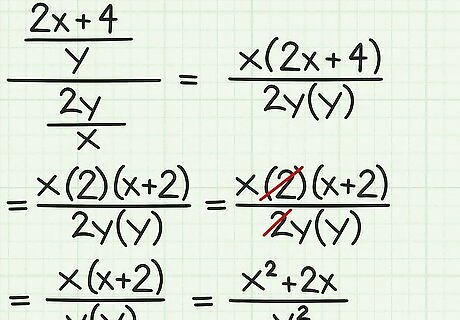
Use the distributive property. You can use the distributive property to factor out a term. This might help you cancel terms. Conversely, you can use the distributive property to multiply a term into a binomial when you are simplifying your expression For example, if you are simplifying the expression 2 x + 4 y 2 y x {\displaystyle {\frac {\frac {2x+4}{y}}{\frac {2y}{x}}}} {\frac {{\frac {2x+4}{y}}}{{\frac {2y}{x}}}}, after taking the reciprocal and combining terms, you end up with the expression x ( 2 x + 4 ) 2 y ( y ) {\displaystyle {\frac {x(2x+4)}{2y(y)}}} {\frac {x(2x+4)}{2y(y)}}. First, factor out a 2 from 2 x + 4 {\displaystyle 2x+4} 2x+4. Then you can cancel a 2 from the numerator and denominator. Then, simplify the expression by completing the multiplication: ( x ) ( 2 ) ( x + 2 ) 2 y ( y ) {\displaystyle {\frac {(x)(2)(x+2)}{2y(y)}}} {\frac {(x)(2)(x+2)}{2y(y)}} ( x ) ( 2 ) ( x + 2 ) 2 y ( y ) {\displaystyle {\frac {(x){\cancel {(2)}}(x+2)}{{\cancel {2}}y(y)}}} {\frac {(x){\cancel {(2)}}(x+2)}{{\cancel {2}}y(y)}} ( x ) ( x + 2 ) y ( y ) {\displaystyle {\frac {(x)(x+2)}{y(y)}}} {\frac {(x)(x+2)}{y(y)}} ( x 2 + 2 x ) y 2 {\displaystyle {\frac {(x^{2}+2x)}{y^{2}}}} {\frac {(x^{{2}}+2x)}{y^{{2}}}} EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher The distributive property helps you avoid repetitive calculations. You can use the distributive property to solve equations where you must multiply a number by a sum or difference. It simplifies calculations, enables expression manipulation (like factoring), and forms the basis for solving many equations.
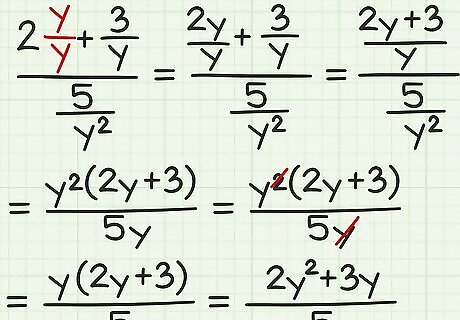
Turn whole numbers into fractions. You will need to do this if the numerator or denominator of the complex fraction contains a whole number being added or subtracted to a fraction. Remember that to add or subtract fractions, the fractions need to have the same denominator. So, to turn a whole number in the top or bottom of a complex fraction into a fraction, multiply it by x x {\displaystyle {\frac {x}{x}}} {\frac {x}{x}}, where x {\displaystyle x} x is the denominator of the fraction it is being added to or subtracted from. For example, if you have 2 + 3 y 5 y 2 {\displaystyle {\frac {2+{\frac {3}{y}}}{\frac {5}{y^{2}}}}} {\frac {2+{\frac {3}{y}}}{{\frac {5}{y^{{2}}}}}}, you would change the 2 into a fraction by multiplying it by y y {\displaystyle {\frac {y}{y}}} {\frac {y}{y}}: 2 + 3 y 5 y 2 {\displaystyle {\frac {2+{\frac {3}{y}}}{\frac {5}{y^{2}}}}} {\frac {2+{\frac {3}{y}}}{{\frac {5}{y^{{2}}}}}} 2 y y + 3 y 5 y 2 {\displaystyle {\frac {{\frac {2y}{y}}+{\frac {3}{y}}}{\frac {5}{y^{2}}}}} {\frac {{\frac {2y}{y}}+{\frac {3}{y}}}{{\frac {5}{y^{{2}}}}}} 2 y + 3 y 5 y 2 {\displaystyle {\frac {\frac {2y+3}{y}}{\frac {5}{y^{2}}}}} {\frac {{\frac {2y+3}{y}}}{{\frac {5}{y^{{2}}}}}} 2 y + 3 y ÷ 5 y 2 {\displaystyle {\frac {2y+3}{y}}\div {\frac {5}{y^{2}}}} {\frac {2y+3}{y}}\div {\frac {5}{y^{{2}}}} 2 y + 3 y × y 2 5 {\displaystyle {\frac {2y+3}{y}}\times {\frac {y^{2}}{5}}} {\frac {2y+3}{y}}\times {\frac {y^{{2}}}{5}} y 2 ( 2 y + 3 ) 5 y {\displaystyle {\frac {y^{2}(2y+3)}{5y}}} {\frac {y^{{2}}(2y+3)}{5y}} y 2 ( 2 y + 3 ) 5 y {\displaystyle {\frac {y^{\cancel {2}}(2y+3)}{5{\cancel {y}}}}} {\frac {y^{{{\cancel {2}}}}(2y+3)}{{5{\cancel {y}}}}} y ( 2 y + 3 ) 5 {\displaystyle {\frac {y(2y+3)}{5}}} {\frac {y(2y+3)}{5}} 2 y 2 + 3 y 5 {\displaystyle {\frac {2y^{2}+3y}{5}}} {\frac {2y^{{2}}+3y}{5}}

















Comments
0 comment