How to Plot Polar Coordinates

Plotting Polar Coordinates

Set up the polar plane. You've probably graphed points with Cartesian coordinates before, using ( x , y ) {\displaystyle (x,y)} (x,y) notation to mark locations on a rectangular grid. Polar coordinates use a different kind of graph instead, based on circles: The center point of the graph (or "origin" in a rectangular grid) is the pole. You can label this with the letter O. Starting from the pole, draw a horizontal line to the right. This is the polar axis. Label the axis with units as you would the positive x-axis on a rectangular grid. If you have special polar graph paper, it will include many circles of different sizes, all centered on the pole. You do not have to draw these yourself if using blank paper.

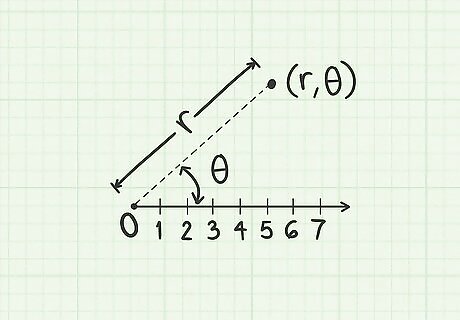
Understand polar coordinates. On the polar plane, a point is represented by a coordinate in the form ( r , θ ) {\displaystyle (r,\theta )} (r,\theta ): The first variable, r {\displaystyle r} r, stands for radius. The point is located on a circle with radius r {\displaystyle r} r, centered on the pole (origin). The second variable, θ {\displaystyle \theta } \theta , represents an angle. The point is located along a line that passes through the pole and forms an angle θ {\displaystyle \theta } \theta with the polar axis.

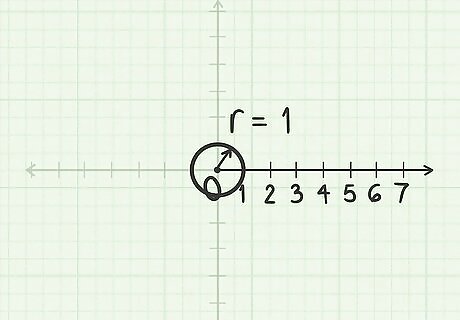
Review the unit circle. In polar coordinates, the angle is usually measured in radians instead of degrees. In this system, one full rotation (360º or a full circle) covers an angle of 2 π {\displaystyle \pi } \pi radians. (This value is chosen because a circle with radius 1 has a circumference of 2 π {\displaystyle \pi } \pi .) Familiarizing yourself with the unit circle will make working with polar coordinates much easier. If your textbook uses degrees, you don't need to worry about this for now. It is possible to plot polar points using degree values for θ {\displaystyle \theta } \theta .

Plotting a Point

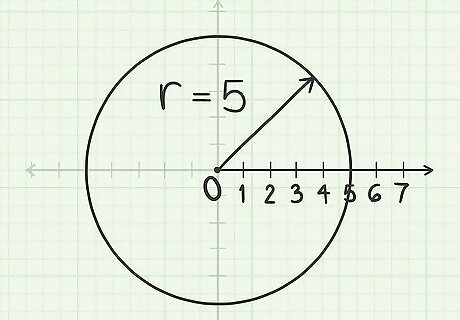
Construct a circle with radius r {\displaystyle r} r. Any point P {\displaystyle P} P has polar coordinates in the form ( r , θ ) {\displaystyle (r,\theta )} (r,\theta ). Begin by drawing a circle with radius r {\displaystyle r} r, centred on the pole. The pole is the center point of the graph, where the origin is on the rectangular coordinate plane. For example, to plot the point ( 5 , π 2 ) {\displaystyle (5,{\frac {\pi }{2}})} (5,{\frac {\pi }{2}}), place your compass on the pole. Extend the pencil end of the compass to 5 units along the polar axis. Rotate the compass to draw a circle.

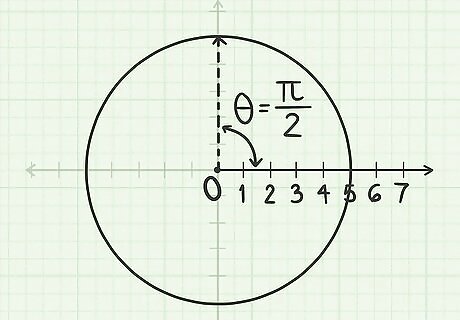
Measure an angle of θ {\displaystyle \theta } \theta from the polar axis. Place a protractor so the center is on the pole, and the edge runs along the polar axis. Measure the angle θ {\displaystyle \theta } \theta from this axis. If the angle is in radians and your protractor only shows degrees, you can convert the units or refer to the unit circle for help. For the point ( 5 , π 2 ) {\displaystyle (5,{\frac {\pi }{2}})} (5,{\frac {\pi }{2}}), the unit circle tells you that π 2 {\displaystyle {\frac {\pi }{2}}} {\frac {\pi }{2}} is ¼ of the way around the circle, equivalent to 90 degrees from the polar axis. Always measure positive angles counter-clockwise from the axis. Measure negative angles clockwise from the axis.

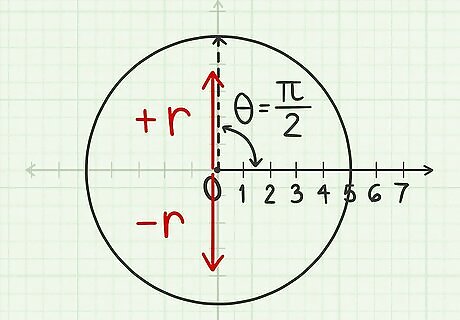
Draw a line based on the sign of r {\displaystyle r} r. The next step will be to draw a line along the angle you measured. Before you can do this, however, you need to know which way to draw the line. Refer back to the polar coordinates ( r , θ ) {\displaystyle (r,\theta )} (r,\theta ) to find out: If r {\displaystyle r} r is positive, draw the line "forward", from the pole straight through the angle marking you just made. If r {\displaystyle r} r is negative, draw the line "backward": from the angle marking back through the pole, to intersect the circle on the opposite side. Don't be confused by rectangular coordinates: this does not correspond to positive or negative values on an x- or y- axis.

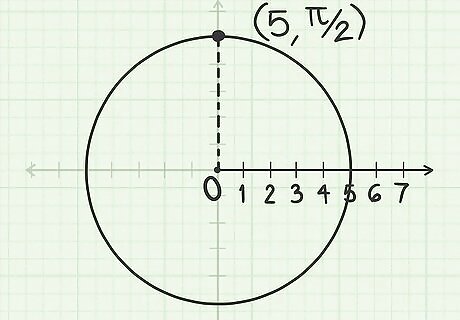
Label the point where the line and circle meet. This is the point ( r , θ ) {\displaystyle (r,\theta )} (r,\theta ). The point ( 5 , π 2 ) {\displaystyle (5,{\frac {\pi }{2}})} (5,{\frac {\pi }{2}}) is located on a circle with radius 5 centered on the pole, ¼ of the way along the circle's circumference in a counter-clockwise direction from the polar axis. (This point is equivalent to (0, 5) in rectangular coordinates.)

Examples

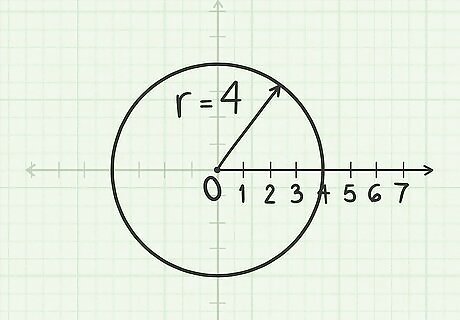
Construct a circle with radius r = 4 {\displaystyle r=4} r=4. Use the pole as its centre.

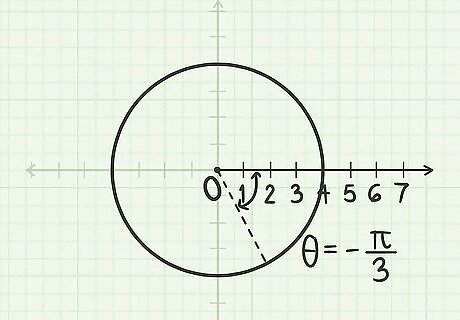
Measure the angle − π 3 {\displaystyle {\frac {-\pi }{3}}} {\frac {-\pi }{3}} radians. Measure this angle from the polar axis (equivalent to the positive x-axis). Since the angle − π 3 {\displaystyle {\frac {-\pi }{3}}} {\frac {-\pi }{3}} is negative, measure this angle in a clockwise direction.

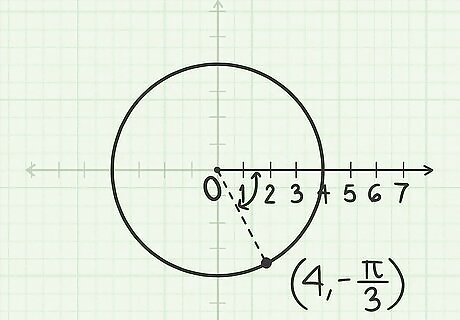
Draw a line at this angle. Start at the pole (origin). Since the radius is positive, move forward from the pole through the angle you measured. The point where the line intersects the circle is ( 4 , − π 3 ) {\displaystyle (4,{\frac {-\pi }{3}})} (4,{\frac {-\pi }{3}}).

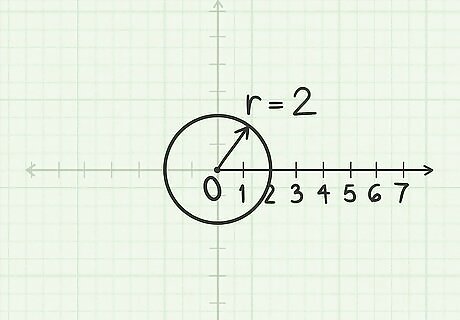
Construct a circle with radius r = 2 {\displaystyle r=2} r=2. Use the pole as its centre. Although the radius is actually -2, the sign is not important for this step.

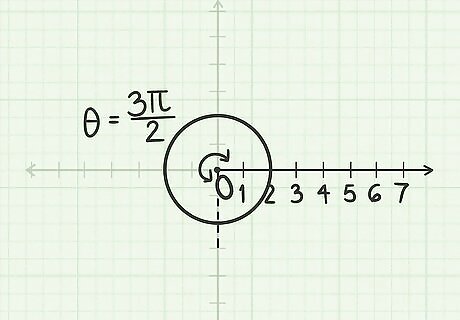
Measure the angle 3 π 2 {\displaystyle {\frac {3\pi }{2}}} {\frac {3\pi }{2}} radians. Since the angle 3 π 2 {\displaystyle {\frac {3\pi }{2}}} {\frac {3\pi }{2}} is positive, you must go counter-clockwise from the polar axis.

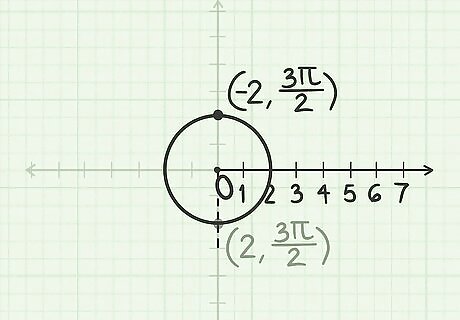
Construct a line opposite that angle. Since the radius − 2 {\displaystyle -2} -2 is negative, you must go from the pole in the opposite direction of the given angle. The point where the line intersects the circle is ( − 2 , 3 π 2 ) {\displaystyle (-2,{\frac {3\pi }{2}})} (-2,{\frac {3\pi }{2}}).

Converting Cartesian Coordinates to Polar Coordinates

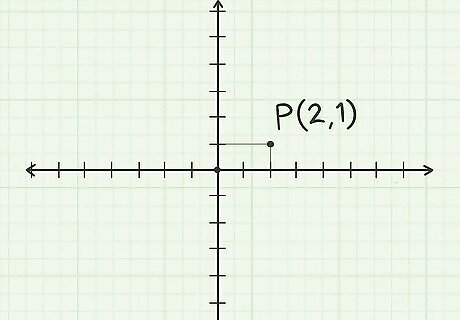
Consider the point P ( 2 , 1 ) {\displaystyle P(2,1)} P(2,1) in the Cartesian plane. Starting at the origin, draw a line segment 2 units along the positive x-axis. Draw a second line segment from that point 1 unit in the positive y direction. You are now at point (2, 1), so label this point P.

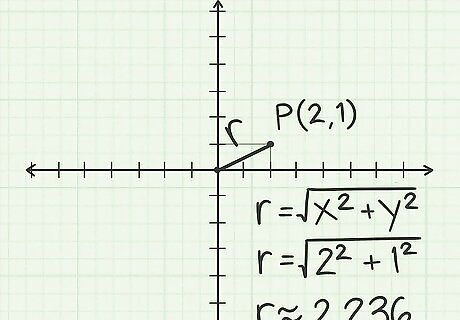
Find the distance between the origin O {\displaystyle O} O and P {\displaystyle P} P. Draw a line between O and P. This line has length r {\displaystyle r} r in polar coordinates. It is also the hypotenuse of a right triangle, so you can find the hypotenuse's length using geometry. For example: The legs of this right triangle have values of 2 and 1. With the Pythagorean theorem, calculate that the hypotenuse's length is 2 2 + 1 2 = 4 + 1 = 5 ≈ 2.236 {\displaystyle {\sqrt {2^{2}+1^{2}}}={\sqrt {4+1}}={\sqrt {5}}\approx 2.236} {\sqrt {2^{{2}}+1^{{2}}}}={\sqrt {4+1}}={\sqrt {5}}\approx 2.236. The general formula to find r {\displaystyle r} r from Cartesian coordinates is r = x 2 + y 2 {\displaystyle r={\sqrt {x^{2}+y^{2}}}} r={\sqrt {x^{{2}}+y^{{2}}}}, where x {\displaystyle x} x is the Cartesian x-coordinate and y {\displaystyle y} y the Cartesian y-coordinate.

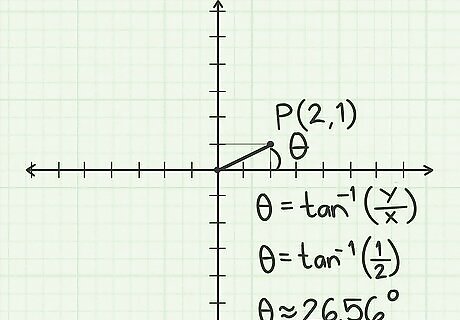
Find the angle between O P {\displaystyle OP} OP and the positive x-axis. Use trigonometry to find this value: tan ⁡ ( θ ) = o p p o s i t e a d j a c e n t = 1 2 {\displaystyle \tan(\theta )={\frac {opposite}{adjacent}}={\frac {1}{2}}} \tan(\theta )={\frac {opposite}{adjacent}}={\frac {1}{2}} tan − 1 ⁡ ( 1 2 ) = θ = 26.56 ∘ {\displaystyle \tan ^{-1}({\frac {1}{2}})=\theta =26.56^{\circ }} \tan ^{{-1}}({\frac {1}{2}})=\theta =26.56^{{\circ }} The general formula to find θ {\displaystyle \theta } \theta is θ = tan − 1 ⁡ ( y x ) {\displaystyle \theta =\tan ^{-1}({\frac {y}{x}})} \theta =\tan ^{{-1}}({\frac {y}{x}}), where y {\displaystyle y} y is the Cartesian y-coordinate and x {\displaystyle x} x the Cartesian x-coordinate.

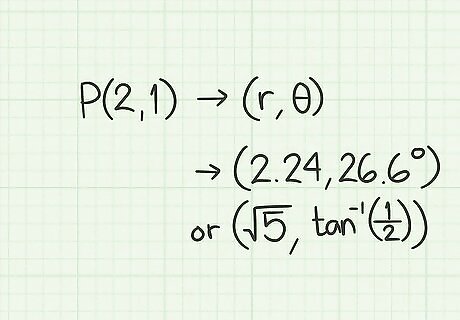
Write down the polar coordinates. You now have the values of r {\displaystyle r} r and θ {\displaystyle \theta } \theta . The rectangular coordinates (2, 1) convert to approximate polar coordinates of (2.24, 26.6º), or exact coordinates of ( 5 , tan − 1 ⁡ ( 1 2 ) ) {\displaystyle ({\sqrt {5}},\tan ^{-1}({\frac {1}{2}}))} ({\sqrt {5}},\tan ^{{-1}}({\frac {1}{2}})).