
views
Prime Tests

Trial division test. Divide n by each prime from 2 to floor( n {\displaystyle {\sqrt {n}}} {\sqrt {n}}).

Fermat's Little Theorem. Warning: false positives are possible, even for all values of a. Choose an integer value for a such that 2 ≤ a ≤ n - 1. If a (mod n) = a (mod n), then n is likely prime. If this is not true, n is not prime. Repeat with different values of a to increase confidence in primality

Miller-Rabin test. Warning: false positives are possible but rarely for multiple values of a. Find values for s and d such that n − 1 = 2 s ∗ d {\displaystyle n-1=2^{s}*d} n-1=2^{s}*d. Choose an integer value for a such that 2 ≤ a ≤ n - 1. If a = +1 (mod n) or -1 (mod n), then n is probably prime. Skip to test result. Otherwise, go to next step. Square your answer ( a 2 d {\displaystyle a^{2d}} a^{{2d}}). If this equals -1 (mod n), then n is probably prime. Skip to test result. Otherwise repeat ( a 4 d {\displaystyle a^{4d}} a^{{4d}} etc.) until a 2 s − 1 d {\displaystyle a^{2^{s-1}d}} a^{{2^{{s-1}}d}}. If you ever square a number which is not ± 1 {\displaystyle \pm 1} \pm 1 (mod n) and end up with +1 (mod n), then n is not prime. If a 2 s − 1 d ≠ ± 1 {\displaystyle a^{2^{s-1}d}\neq \pm 1} a^{{2^{{s-1}}d}}\neq \pm 1 (mod n), then n is not prime. Test result: If n passes test, repeat with different values of a to increase confidence.
Understanding Prime Testing

Understand the trial division method. By the definition of primality, n is only prime if it cannot be divided evenly by integers 2 or greater. The formula given saves time by removing unnecessary tests (e.g. after testing 3 there is no need to test 9). Floor(x) rounds x to the closest integer ≤ x.
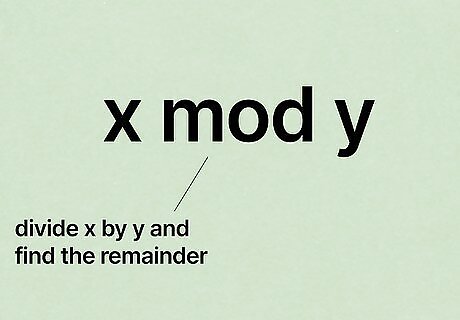
Understand modular arithmetic. The "x mod y" operation (short for "modulo") means "divide x by y and find the remainder." In other words, in modular arithmetic, numbers "wrap around" back to zero upon reaching a certain value, called the modulus. A clock counts in modulo 12: it goes from 10 to 11 to 12, then wraps around back to 1. Many calculators have a mod button, but see the end of this section for how to solve this by hand for large numbers.

Know the pitfalls of Fermat's Little Theorem. All numbers that fail this test are composite (non-prime), but unfortunately numbers that pass this test are only likely primes. If you want to be sure of avoiding false positives, look for n on a list of "Carmichael numbers" (which pass this test every time) and "Fermat pseudoprimes" (which pass this test only for some values of a).

Use the Miller-Rabin test whenever practical. Although tedious to perform by hand, this test is commonly used in software. This can be performed at a practical speed and gives fewer false positives than Fermat's method. A composite number never gives a false positive for more than ¼ of the values of a. If you choose several values of a at random and they all pass this test, you can be fairly confident that n is prime.

Perform modular arithmetic for large numbers. If you do not have access to a calculator with a mod function, or if your calculator can't display numbers that high, use properties of exponents and modular arithmetic to make the process easier. Here's an example for 3 50 {\displaystyle 3^{50}} 3^{{50}} mod 50: Rewrite the expression with more manageable exponents: ( 3 25 ∗ 3 25 ) {\displaystyle (3^{25}*3^{25})} (3^{{25}}*3^{{25}}) mod 50. (You may need to break it down further if calculating by hand). ( 3 25 ∗ 3 25 ) {\displaystyle (3^{25}*3^{25})} (3^{{25}}*3^{{25}}) mod 50 = ( 3 25 {\displaystyle (3^{25}} (3^{{25}} mod 50 ∗ 3 25 {\displaystyle *3^{25}} *3^{{25}} mod 50) mod 50. (This is a property of modular multiplication.) 3 25 {\displaystyle 3^{25}} 3^{{25}} mod 50 = 43. ( 3 25 {\displaystyle (3^{25}} (3^{{25}} mod 50 ∗ 3 25 {\displaystyle *3^{25}} *3^{{25}} mod 50) mod 50 = ( 43 ∗ 43 ) {\displaystyle (43*43)} (43*43) mod 50 = 1849 {\displaystyle =1849} =1849 mod 50 = 49 {\displaystyle =49} =49
Chinese Remainder Theorem Test

Choose two numbers. One of the numbers is not prime and the second number is the number that needs to be tested for primality. "Prime1" = 35 Prime2 = 97

Choose two datapoints that are greater than zero and less than prime1 and prime2 respectfully. They can't equal each other. Data1 = 1 Data2 = 2

Calculate MMI (Mathematical Multiplicative Inverse) for Prime1 and Prime2 Calculate MMI MMI1 = Prime2 ^ -1 Mod Prime1 MMI2 = Prime1 ^ -1 Mod Prime2 For Prime Numbers only (it will give a number for non-prime numbers but it won't be its MMI): MMI1 = (Prime2 ^ (Prime1-2)) % Prime1 MMI2 = (Prime1 ^ (Prime2-2)) % Prime2 e.g MMI1 = (97 ^ 33) % 35 MMI2 = (35 ^ 95) % 97
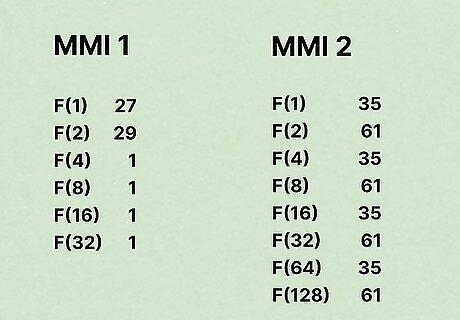
Create a binary table for each MMI up to Log2 of the Modulus For MMI1 F(1) = Prime2 % Prime1 = 97 % 35 = 27 F(2) = F(1) * F(1) % Prime1 = 27 * 27 % 35 = 29 F(4) = F(2) * F(2) % Prime1 = 29 * 29 % 35 = 1 F(8) = F(4) * F(4) % Prime1 = 1 * 1 % 35 = 1 F(16) =F(8) * F(8) % Prime1 = 1 * 1 % 35 = 1 F(32) =F(16) * F(16) % Prime1 = 1 * 1 % 35 = 1 Calculate the binary of Prime1 - 2 35 -2 = 33 (10001) base 2 MMI1 = F(33) = F(32) * F(1) mod 35 MMI1 = F(33) = 1 * 27 Mod 35 MMI1 = 27 For MMI2 F(1) = Prime1 % Prime2 = 35 % 97 = 35 F(2) = F(1) * F(1) % Prime2 = 35 * 35 mod 97 = 61 F(4) = F(2) * F(2) % Prime2 = 61 * 61 mod 97 = 35 F(8) = F(4) * F(4) % Prime2 = 35 * 35 mod 97 = 61 F(16) = F(8) * F(8) % Prime2 = 61 * 61 mod 97 = 35 F(32) = F(16) * F(16) % Prime2 = 35 * 35 mod 97 = 61 F(64) = F(32) * F(32) % Prime2 = 61 * 61 mod 97 = 35 F(128) = F(64) * F(64) % Prime2 = 35 * 35 mod 97 = 61 Calculate the binary of Prime2 - 2 97 - 2 = 95 = (1011111) base 2 MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97) MMI2 = (((((35 * 35) %97) * 61) % 97) * 35 % 97) * 61 % 97) * 35 % 97) MMI2 = 61

Calculate (Data1 * Prime2 * MMI1 + Data2 * Prime1 * MMI2) % (Prime1 * Prime2) Answer = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35) Answer = (2619 + 4270) % 3395 Answer = 99

Verify that "Prime1" is not Prime Calculate (Answer - Data1) % Prime1 99 -1 % 35 = 28 Since 28 is greater than 0, 35 is not prime

Check if Prime2 is Prime Calculate (Answer - Data2) % Prime2 99 - 2 % 97 = 0 Since 0 equals 0, 97 is potentially prime
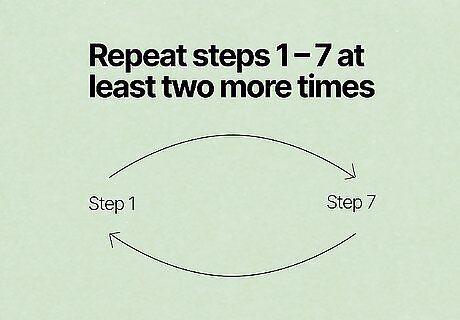
Repeat steps 1 through 7 at least two more times. If step 7 is 0: Use a different "prime1" where prime1 is a non-prime Use a different prime 1 where prime 1 is an actual prime. In this case, steps 6 and 7 should equal 0. Use different data points for data1 and data2. If step 7 is 0 every time, there is an extremely high probability that prime2 is prime. Steps 1 though 7 are known to fail in certain cases when the first number is a non-prime number and the second prime is a factor of the non-prime number "prime1". It works in all scenarios where both numbers are prime. The reason why steps 1 though 7 are repeated is because there are a few scenarios where, even if prime1 is not prime and prime2 is not prime, step 7 still works out to be zero, for one or both the numbers. These circumstances are rare. By changing prime1 to a different non-prime number, if prime2 is not prime, prime2 will rapidly not equal zero in step 7. Except for the instance where "prime1" is a factor of prime2, prime numbers will always equal zero in step 7.



















Comments
0 comment