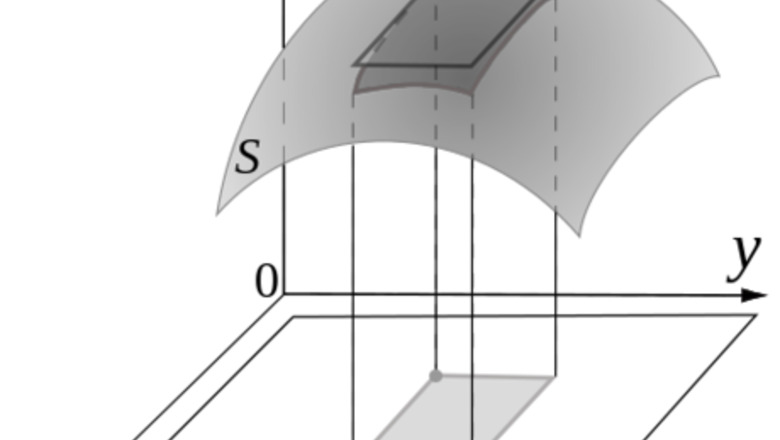
views
The surface element
d
S
{\displaystyle \mathrm {d} \mathbf {S} }
contains information on both the area and the orientation of the surface. Below, we derive the surface element in the standard Cartesian coordinate system and give an example on how to evaluate surface integrals.
Deriving the Surface Element
Consider an arbitrary vector function r {\displaystyle \mathbf {r} } {\mathbf {r}}. Below, we let z = f ( x , y ) . {\displaystyle z=f(x,y).} z=f(x,y). r = x i + y j + f ( x , y ) k {\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +f(x,y)\mathbf {k} } {\mathbf {r}}=x{\mathbf {i}}+y{\mathbf {j}}+f(x,y){\mathbf {k}}
Calculate differentials. For d r x , y {\displaystyle \mathrm {d} \mathbf {r} _{x},\,y} {\mathrm {d}}{\mathbf {r}}_{{x}},\,y is being held constant, and vice versa. We use the notation f x = ∂ f ( x , y ) ∂ x . {\displaystyle f_{x}={\frac {\partial f(x,y)}{\partial x}}.} f_{{x}}={\frac {\partial f(x,y)}{\partial x}}. d r x = d x i + f x d x k {\displaystyle \mathrm {d} \mathbf {r} _{x}=\mathrm {d} x\mathbf {i} +f_{x}\mathrm {d} x\mathbf {k} } {\mathrm {d}}{\mathbf {r}}_{{x}}={\mathrm {d}}x{\mathbf {i}}+f_{{x}}{\mathrm {d}}x{\mathbf {k}} d r y = d y j + f y d y k {\displaystyle \mathrm {d} \mathbf {r} _{y}=\mathrm {d} y\mathbf {j} +f_{y}\mathrm {d} y\mathbf {k} } {\mathrm {d}}{\mathbf {r}}_{{y}}={\mathrm {d}}y{\mathbf {j}}+f_{{y}}{\mathrm {d}}y{\mathbf {k}}
Take the cross product of the two differentials. d S = d r x × d r y = | i j k d x 0 f x d x 0 d y f y d y | = − f x d x d y i − f y d x d y j + d x d y k {\displaystyle {\begin{aligned}\mathrm {d} \mathbf {S} &=\mathrm {d} \mathbf {r} _{x}\times \mathrm {d} \mathbf {r} _{y}\\&={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\mathrm {d} x&0&f_{x}\mathrm {d} x\\0&\mathrm {d} y&f_{y}\mathrm {d} y\end{vmatrix}}\\&=-f_{x}\mathrm {d} x\mathrm {d} y\mathbf {i} -f_{y}\mathrm {d} x\mathrm {d} y\mathbf {j} +\mathrm {d} x\mathrm {d} y\mathbf {k} \end{aligned}}} {\begin{aligned}{\mathrm {d}}{\mathbf {S}}&={\mathrm {d}}{\mathbf {r}}_{{x}}\times {\mathrm {d}}{\mathbf {r}}_{{y}}\\&={\begin{vmatrix}{\mathbf {i}}&{\mathbf {j}}&{\mathbf {k}}\\{\mathrm {d}}x&0&f_{{x}}{\mathrm {d}}x\\0&{\mathrm {d}}y&f_{{y}}{\mathrm {d}}y\end{vmatrix}}\\&=-f_{{x}}{\mathrm {d}}x{\mathrm {d}}y{\mathbf {i}}-f_{{y}}{\mathrm {d}}x{\mathrm {d}}y{\mathbf {j}}+{\mathrm {d}}x{\mathrm {d}}y{\mathbf {k}}\end{aligned}} d S = ( − f x i − f y j + k ) d x d y {\displaystyle \mathrm {d} \mathbf {S} =(-f_{x}\mathbf {i} -f_{y}\mathbf {j} +\mathbf {k} )\mathrm {d} x\mathrm {d} y} {\mathrm {d}}{\mathbf {S}}=(-f_{{x}}{\mathbf {i}}-f_{{y}}{\mathbf {j}}+{\mathbf {k}}){\mathrm {d}}x{\mathrm {d}}y The formula above is the surface element for general surfaces defined by z = f ( x , y ) . {\displaystyle z=f(x,y).} z=f(x,y). It is important to note that the nature of surfaces (more accurately, the cross product) still allows one ambiguity - the way the normal vector is pointing. The result that we have derived applies to outward normals, as recognized by the positive k {\displaystyle \mathbf {k} } {\mathbf {k}} component, and for most applications, this will always be the case. The derivation works in any coordinate system. See the tips for the derivation in cylindrical coordinates.
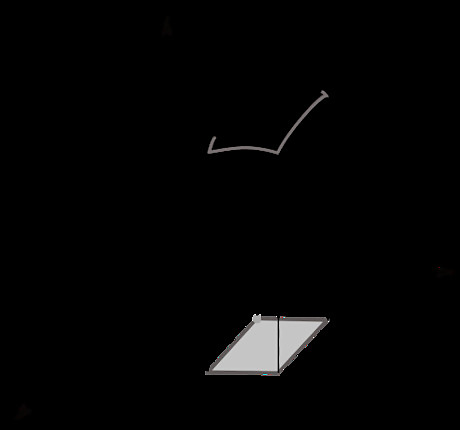
Visualize a surface integral. The surface consists of infinitesimal patches that are approximately flat. As you can see, the way we integrate over a domain works the same way, and the fact that a surface element denotes orientation as well reflects that surface integrals are a powerful generalization of area integrals.
Surface Area
Calculate the surface area of the function z = 4 − x 2 − y 2 {\displaystyle z=4-x^{2}-y^{2}} z=4-x^{{2}}-y^{{2}} above the xy-plane. Finding the surface area involves finding the integral below. We only care about the area of the surface, not its orientation, so we find its magnitude. ∫ S | d S | = ∫ A 1 + ( ∂ z ∂ x ) 2 + ( ∂ z ∂ y ) 2 d A {\displaystyle \int _{S}|\mathrm {d} \mathbf {S} |=\int _{A}{\sqrt {1+\left({\frac {\partial z}{\partial x}}\right)^{2}+\left({\frac {\partial z}{\partial y}}\right)^{2}}}\,\mathrm {d} A} \int _{{S}}|{\mathrm {d}}{\mathbf {S}}|=\int _{{A}}{\sqrt {1+\left({\frac {\partial z}{\partial x}}\right)^{{2}}+\left({\frac {\partial z}{\partial y}}\right)^{{2}}}}\,{\mathrm {d}}A
Find the magnitude of the surface element. Recall from part 1 that d S = ( − f x i − f y j + k ) d A , {\displaystyle \mathrm {d} \mathbf {S} =(-f_{x}\mathbf {i} -f_{y}\mathbf {j} +\mathbf {k} )\mathrm {d} A,} {\mathrm {d}}{\mathbf {S}}=(-f_{{x}}{\mathbf {i}}-f_{{y}}{\mathbf {j}}+{\mathbf {k}}){\mathrm {d}}A, where z = f ( x , y ) . {\displaystyle z=f(x,y).} z=f(x,y). d S = 2 x i + 2 y j + k {\displaystyle \mathrm {d} \mathbf {S} =2x\mathbf {i} +2y\mathbf {j} +\mathbf {k} } {\mathrm {d}}{\mathbf {S}}=2x{\mathbf {i}}+2y{\mathbf {j}}+{\mathbf {k}} | d S | = 4 x 2 + 4 y 2 + 1 d A {\displaystyle |\mathrm {d} \mathbf {S} |={\sqrt {4x^{2}+4y^{2}+1}}\mathrm {d} A} |{\mathrm {d}}{\mathbf {S}}|={\sqrt {4x^{{2}}+4y^{{2}}+1}}{\mathrm {d}}A
Set the boundaries. The boundary on the xy-plane is a circle of radius 2. This means that we should evaluate in polar coordinates too. ∫ S | d S | = ∫ 0 2 r d r ∫ 0 2 π d θ 4 r 2 + 1 {\displaystyle \int _{S}|\mathrm {d} \mathbf {S} |=\int _{0}^{2}r\mathrm {d} r\int _{0}^{2\pi }\mathrm {d} \theta {\sqrt {4r^{2}+1}}} \int _{{S}}|{\mathrm {d}}{\mathbf {S}}|=\int _{{0}}^{{2}}r{\mathrm {d}}r\int _{{0}}^{{2\pi }}{\mathrm {d}}\theta {\sqrt {4r^{{2}}+1}}
Evaluate using any means possible. U-substitution is the way to go. ∫ S | d S | = 2 π ∫ 0 2 r 4 r 2 + 1 d r , u = 1 + 4 r 2 = π 4 ∫ 1 17 u 1 / 2 d u = π 6 ( 17 3 / 2 − 1 ) {\displaystyle {\begin{aligned}\int _{S}|\mathrm {d} \mathbf {S} |&=2\pi \int _{0}^{2}r{\sqrt {4r^{2}+1}}\mathrm {d} r,\ \ \ u=1+4r^{2}\\&={\frac {\pi }{4}}\int _{1}^{17}u^{1/2}\mathrm {d} u\\&={\frac {\pi }{6}}(17^{3/2}-1)\end{aligned}}} {\begin{aligned}\int _{{S}}|{\mathrm {d}}{\mathbf {S}}|&=2\pi \int _{{0}}^{{2}}r{\sqrt {4r^{{2}}+1}}{\mathrm {d}}r,\ \ \ u=1+4r^{{2}}\\&={\frac {\pi }{4}}\int _{{1}}^{{17}}u^{{1/2}}{\mathrm {d}}u\\&={\frac {\pi }{6}}(17^{{3/2}}-1)\end{aligned}}

















Comments
0 comment