How to Calculate Maximum Revenue

Using the Revenue Function

Understand the relation between price and demand. Economics study shows that, for most traditional businesses, as the demand for any item increases, the price for that item should decrease. Conversely, as the price decreases, demand should increase. Using data from actual sales, a company can determine a supply and demand graph. That data can be used to calculate a price function. For more information on graphing supply and demand data, see Find and Analyze Demand Function Curve. Make sure you understand how to construct a Price-Demand function from your real scenario. It's important to consider the following: Historical data: Analyze past sales data to determine how price changes have impacted demand. Competitive Analysis: Look at how competitors price similar products and how it affects their sales. Consumer Surveys: Directly ask how consumers might respond to different pricing scenarios. Economic Conditions: Current economic conditions can influence consumer purchasing power and spending willingness. Substitutes and Complements: The availability and pricing of substitute or complementary products can affect demand.

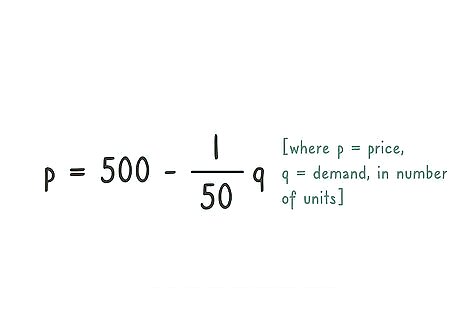
Create a price function. The price function consists of two primary pieces of information. The first is the intercept. This is the theoretical price if no items are sold. The second detail is a decreasing slope. The slope of the graph represents the drop in price for each item. A sample price function might look like: p = 500 − 1 50 q {\displaystyle p=500-{\frac {1}{50}}q} p=500-{\frac {1}{50}}q p = price q = demand, in number of units This function sets the “zero price” at $500. For each unit sold, the price decreases by 1/50th of a dollar (two cents).

Determine the revenue function. Revenue is the product of price times the number of units sold. Since the price function includes the number of units, this will result in a squared variable. Using the price function from above, the revenue function becomes: R ( q ) = p ∗ q {\displaystyle R(q)=p*q} R(q)=p*q R ( q ) = [ 500 − 1 50 q ] ∗ q {\displaystyle R(q)=[500-{\frac {1}{50}}q]*q} R(q)=[500-{\frac {1}{50}}q]*q R ( q ) = 500 q − 1 50 q 2 {\displaystyle R(q)=500q-{\frac {1}{50}}q^{2}} R(q)=500q-{\frac {1}{50}}q^{2}

Finding the Maximum Revenue Value

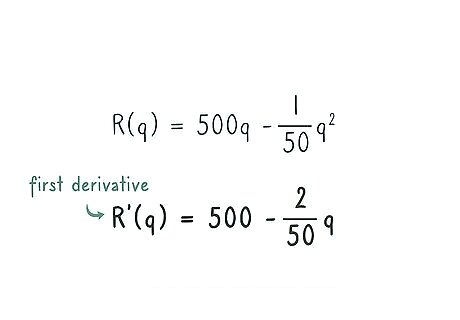
Find the first derivative of the revenue function. In calculus, the derivative of any function is used to find the rate of change of that function. The maximum value of a given function occurs when the derivative equals zero. So, to maximize the revenue, find the first derivative of the revenue function. Suppose the revenue function, in terms of number of units sold, is R ( q ) = 500 q − 1 50 q 2 {\displaystyle R(q)=500q-{\frac {1}{50}}q^{2}} R(q)=500q-{\frac {1}{50}}q^{2}. The first derivative, therefore, is: R ′ ( q ) = 500 − 2 50 q {\displaystyle R^{\prime }(q)=500-{\frac {2}{50}}q} R^{{\prime }}(q)=500-{\frac {2}{50}}q For a review of derivatives, see the wikiHow article on how to Take Derivatives.

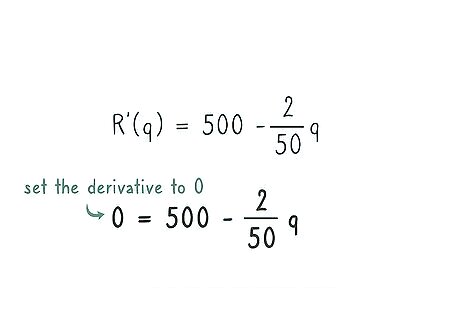
Set the derivative equal to 0. When the derivative is zero, the graph of the original function is at either a peak or a trough. This will be either the maximum or minimum value. For some higher level functions, there may be more than one solution to the zero derivative, but not a basic price-demand function. R ′ ( q ) = 500 − 2 50 q {\displaystyle R^{\prime }(q)=500-{\frac {2}{50}}q} R^{{\prime }}(q)=500-{\frac {2}{50}}q 0 = 500 − 2 50 q {\displaystyle 0=500-{\frac {2}{50}}q} 0=500-{\frac {2}{50}}q

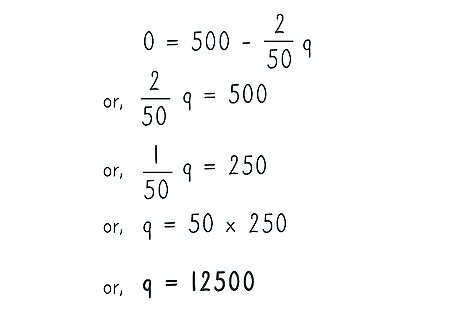
Solve for the number of items at the 0 value. Use basic algebra to solve the derivative for the number of items to sell where the derivative is equal to zero. This will give you the number of items that will maximize the revenue. 0 = 500 − 2 50 q {\displaystyle 0=500-{\frac {2}{50}}q} 0=500-{\frac {2}{50}}q 2 50 q = 500 {\displaystyle {\frac {2}{50}}q=500} {\frac {2}{50}}q=500 1 50 q = 250 {\displaystyle {\frac {1}{50}}q=250} {\frac {1}{50}}q=250 q = 50 ∗ 250 {\displaystyle q=50*250} q=50*250 q = 12 , 500 {\displaystyle q=12,500} q=12,500

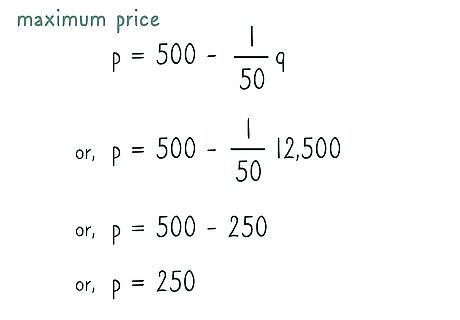
Calculate the maximum price. Using the optimal number of sales from the derivative calculation, you can enter that value into the original price formula to find the optimal price. p = 500 − 1 50 q {\displaystyle p=500-{\frac {1}{50}}q} p=500-{\frac {1}{50}}q p = 500 − 1 50 12 , 500 {\displaystyle p=500-{\frac {1}{50}}12,500} p=500-{\frac {1}{50}}12,500 p = 500 − 250 {\displaystyle p=500-250} p=500-250 p = 250 {\displaystyle p=250} p=250

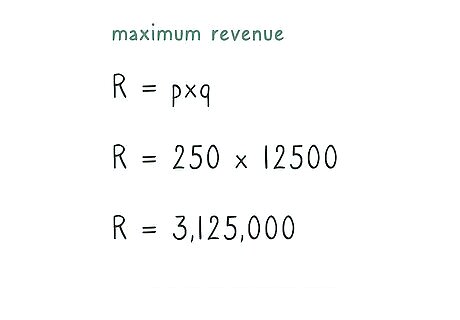
Combine the results to calculate maximum revenue. After you have found the optimal number of sales and the optimal price, multiply them to find the maximum revenue. Recall that R = p ∗ q {\displaystyle R=p*q} R=p*q. The maximum revenue for this example, therefore, is: R = p ∗ q {\displaystyle R=p*q} R=p*q R = ( 250 ) ( 12 , 500 ) {\displaystyle R=(250)(12,500)} R=(250)(12,500) R = 3 , 125 , 000 {\displaystyle R=3,125,000} R=3,125,000

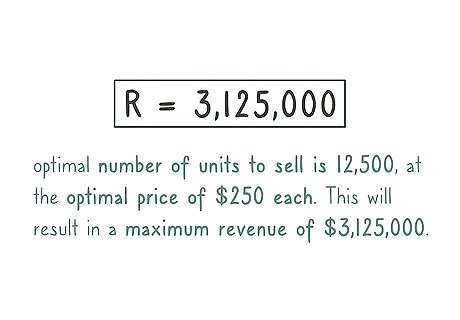
Summarize the results. Based on these calculations, the optimal number of units to sell is 12,500, at the optimal price of $250 each. This will result in a maximum revenue, for this sample problem, of $3,125,000.

Solving Another Sample Problem

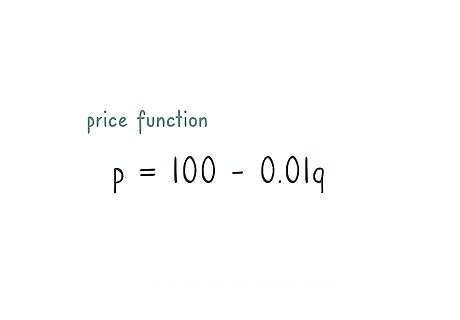
Begin with the price function. Suppose that another business has collected price and sales data. Using that data, the company has determined that the initial price is $100, and each additional unit sold will cut the price by one cent. Using this data, the following price function is: p = 100 − 0.01 q {\displaystyle p=100-0.01q} p=100-0.01q

Determine the revenue function. Recall that revenue is equal to price times quantity. Using the price function above, the revenue function is: R ( q ) = [ 100 − 0.01 q ] ∗ q {\displaystyle R(q)=[100-0.01q]*q} R(q)=[100-0.01q]*q R ( q ) = 100 q − 0.01 q 2 {\displaystyle R(q)=100q-0.01q^{2}} R(q)=100q-0.01q^{2}

Find the derivative of the revenue function. Using basic calculus, find the derivative of the revenue function: R ( q ) = 100 q − 0.01 q 2 {\displaystyle R(q)=100q-0.01q^{2}} R(q)=100q-0.01q^{2} R ′ ( q ) = 100 − ( 2 ) 0.01 q {\displaystyle R^{\prime }(q)=100-(2)0.01q} R^{{\prime }}(q)=100-(2)0.01q R ′ ( q ) = 100 − 0.02 q {\displaystyle R^{\prime }(q)=100-0.02q} R^{{\prime }}(q)=100-0.02q

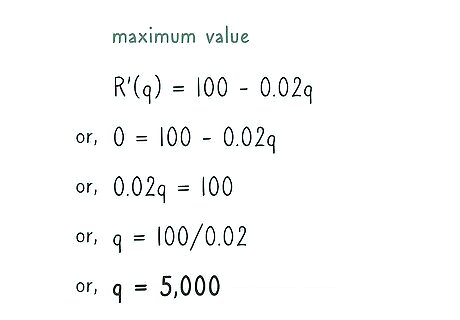
Find the maximum value. Set the derivative equal to zero and solve for q {\displaystyle q} q to find the optimal number of sales. This calculation is as follows: R ′ ( q ) = 100 − 0.02 q {\displaystyle R^{\prime }(q)=100-0.02q} R^{{\prime }}(q)=100-0.02q 0 = 100 − 0.02 q {\displaystyle 0=100-0.02q} 0=100-0.02q 0.02 q = 100 {\displaystyle 0.02q=100} 0.02q=100 q = 100 / 0.02 {\displaystyle q=100/0.02} q=100/0.02 q = 5 , 000 {\displaystyle q=5,000} q=5,000

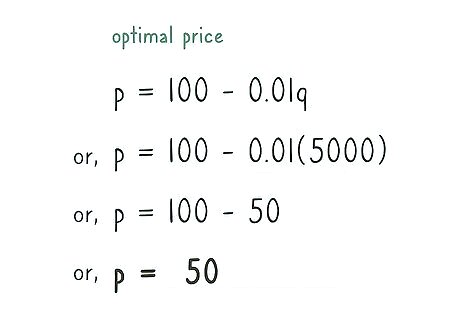
Calculate the optimal price. Use the optimal sales value in the original price formula to find the optimal sales price. For this example, this works as follows: p = 100 − 0.01 q {\displaystyle p=100-0.01q} p=100-0.01q p = 100 − 0.01 ( 5 , 000 ) {\displaystyle p=100-0.01(5,000)} p=100-0.01(5,000) p = 100 − 50 {\displaystyle p=100-50} p=100-50 p = 50 {\displaystyle p=50} p=50

Combine the maximum sales and optimal price to find maximum revenue. Using the relationship that revenue equals price times quantity, you can find the maximum revenue as follows: R ( q ) = p ∗ q {\displaystyle R(q)=p*q} R(q)=p*q R ( q ) = 50 ∗ 5 , 000 {\displaystyle R(q)=50*5,000} R(q)=50*5,000 R ( q ) = 250 , 000 {\displaystyle R(q)=250,000} R(q)=250,000

Interpret the results. Using this data and based on the price function p = 100 − 0.01 q {\displaystyle p=100-0.01q} p=100-0.01q, the company’s maximum revenue is $250,000. This assumes a unit price of $50 and a sale of 5,000 units.