
views
Calculating Fluid Pressure

Set up the equation. The equation for fluid pressure is independent of the mass or volume of the liquid. Instead, fluid pressure is the product of the density of the liquid, the height of the liquid above the object, and gravity. Since gravity and liquid densities are fixed (for the most part), the height of the liquid is the largest variable in the equation. The equation reads as Pfluid = ρgh, where ρ is the density of the liquid, g is the acceleration of gravity, and h is the height of the liquid (or depth of the fluid).

Multiply the variables. To solve the equation, you take the product of the three variables. You can use a calculator, or do the calculations on your own. There are also online calculators that will do this calculation for you. For example, if you had a fluid that with a density of (1.08 x 10 kg/m) and was 5.00 m high, you would multiply (1.08 x 10 kg/m) x 9.81 m/s (acceleration of gravity on Earth) x 5.00 m. In this case, you would get the answer of 5.30 x 10.
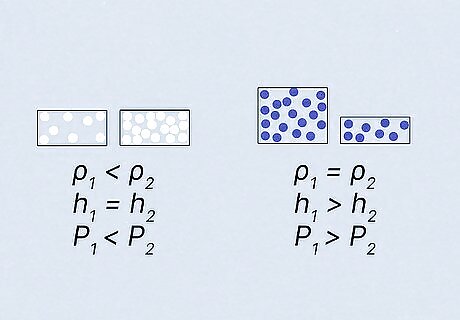
Analyze your results. Make sure that your results add up logically. You should not get a reading for negative fluid pressure. You also should compare different measurements to see if they follow the expected trends. For example, more dense liquids will exert more pressure at the same height. The same liquid will exert more pressure when the height is higher. Since water is more dense than oil, you can expect water to exert more fluid pressure than oil at the same height.
Finding the Density of your Liquid
Measure the volume of your liquid. Pour 100 mL of liquid into a pre-weighed graduated cylinder. Make sure that your measurement is correct, and then write the volume down as 100 mL. You can write in a lab journal or notebook.
Weigh the liquid. Put the sample of liquid on a scale. Measure the mass of 100 mL of your liquid. You can tare the scale (zero it out) with the empty graduated cylinder on it before adding the liquid, or subtract the weight of the graduated cylinder from the total weight to obtain the mass of your liquid. The measurement shown on the scale is the total mass of the liquid and the cylinder.
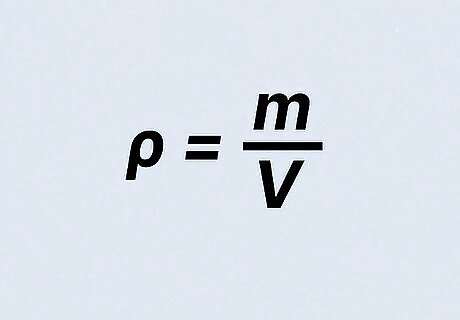
Calculate the liquid’s density. Density is equal to the mass of the liquid divided by the volume of the liquid. In this case, you have measured both. You will simply divide the mass by 100 mL. For example, if your liquid had a mass of 125 g, you would divide that by 100 mL. Your resulting answer would be 1.25 g/mL. However, make sure to pay close attention to the desired units of measurement. You may need to find the gallons per Liter (g/L) instead.
Understanding the Concepts
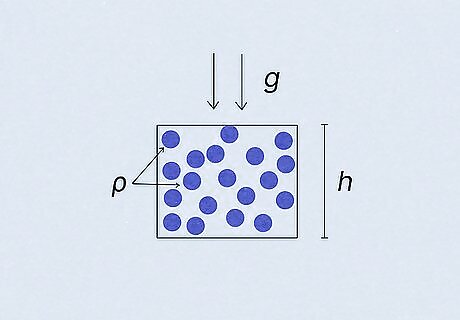
Consider the meaning of each variable. The density of the liquid is significant because it tells you how much mass your liquid has per unit of volume. Gravity then exerts a force on that mass to pull it down. Finally, the height of the liquid tells you how much liquid is above the object experiencing the pressure.

Study the units involved. The units for fluid pressure are pascals or sometimes millimeters of mercury (mmHg). The pascal is an S.I. unit for pressure. The mmHg unit (and similar units that denote a height of some liquid) comes from the dependency of pressure on height.
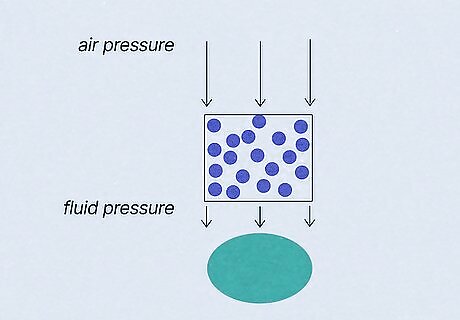
See fluid pressure as one force acting on an object. The force that is exerted on some object by fluid pressure is only one force. There could many forces acting on the same object. For example, air pressure and fluid pressure are often added together to obtain a “total pressure” acting on some object.
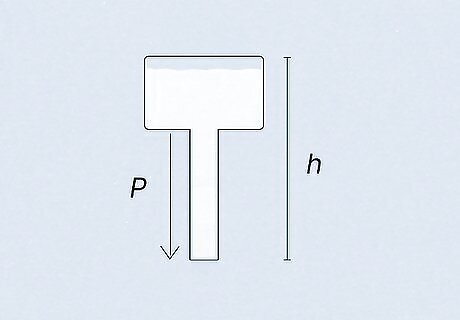
Apply fluid pressure concepts. Once you have calculated fluid pressure for a liquid or set of liquids, you can use them for varying applications. For example, understanding the fluid pressure of water would be important to building a water tower that can hold water at a certain height. This is also important for use in mercury thermometers, or other systems that use liquids as measurements.













Comments
0 comment