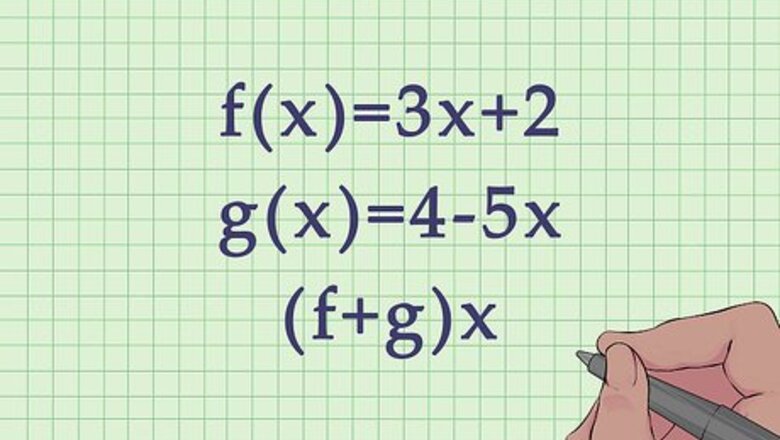
views
Adding or Subtracting Functions without an Input
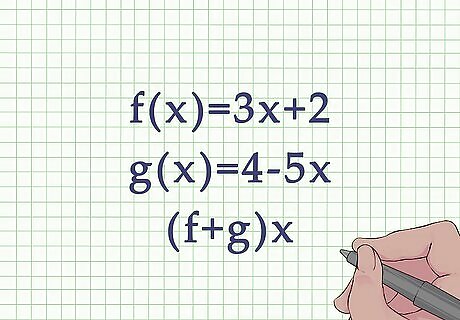
Write out the functions that are being added or subtracted. Functions are usually stated as f(x) = relationship, where x is the variable input, and the relationship is stated as a formula for the variable x. Since you are adding or subtracting more than one function, they will be labeled differently, most likely f ( x ) {\displaystyle f(x)} f(x) and g ( x ) {\displaystyle g(x)} g(x). For example, you might be asked to add the function f ( x ) = 3 x + 2 {\displaystyle f(x)=3x+2} f(x)=3x+2, and the function g ( x ) = 4 − 5 x {\displaystyle g(x)=4-5x} g(x)=4-5x. If you are being asked to add, you will often be asked to find ( f + g ) x {\displaystyle (f+g)x} (f+g)x. If you are being asked to subtract, you will often be asked to find ( f − g ) x {\displaystyle (f-g)x} (f-g)x.
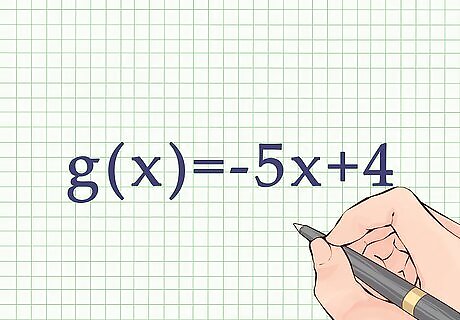
Reorder the functions by degree of terms. This means ordering the formula by exponents, beginning with the largest exponent ( x 3 , x 2 , x , {\displaystyle x^{3},x^{2},x,} x^{{3}},x^{{2}},x, etc.). If there is no exponent, order the first-degree term first (x), followed the constants (numbers without variables). For example, the function g ( x ) {\displaystyle g(x)} g(x) would be reordered as − 5 x + 4 {\displaystyle -5x+4} -5x+4. The f(x) function is already ordered by degree of terms.
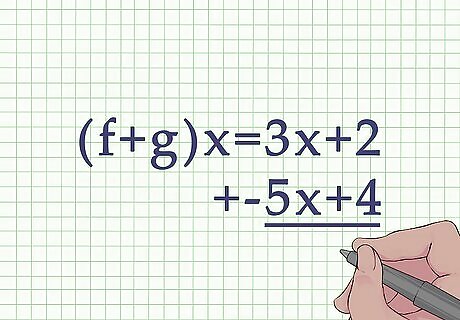
Create an addition or subtraction problem using the two formulas. You can add/subtract horizontally or vertically, since you have ordered the functions by terms. For example, your function can be set up as ( f + g ) x = ( 3 x + 2 ) + ( − 5 x + 4 ) {\displaystyle (f+g)x=(3x+2)+(-5x+4)} (f+g)x=(3x+2)+(-5x+4), or it could be set up vertically, with like terms lined up: + 3 x + 2 − 5 x + 4 {\displaystyle +{\begin{matrix}3x&+&2\\-5x&+&4\end{matrix}}} +{\begin{matrix}3x&+&2\\-5x&+&4\end{matrix}}.
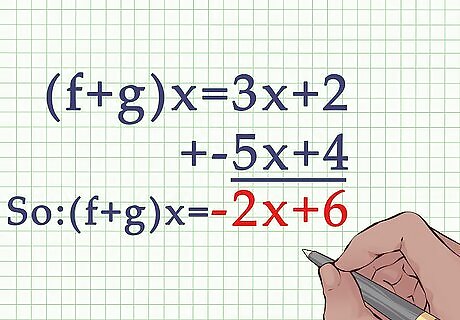
Add or subtract like terms. It is helpful to add/subtract in order of the degree of terms, beginning with the highest exponent (if any). For example, for ( f + g ) x = ( 3 x + 2 ) + ( − 5 x + 4 ) {\displaystyle (f+g)x=(3x+2)+(-5x+4)} (f+g)x=(3x+2)+(-5x+4), you would first add the first-degree terms: 3 x + ( − 5 x ) = − 2 x {\displaystyle 3x+(-5x)=-2x} 3x+(-5x)=-2x.Second, you would add the constants: 2 + 4 = 6 {\displaystyle 2+4=6} 2+4=6.So ( f + g ) x = − 2 x + 6 {\displaystyle (f+g)x=-2x+6} (f+g)x=-2x+6.
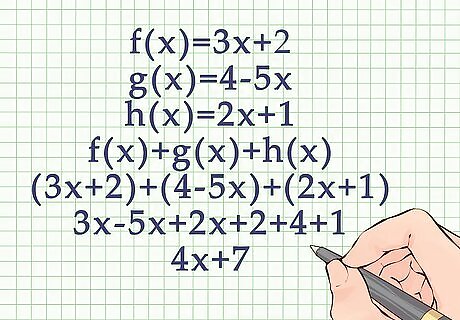
Follow the same process for adding or subtracting more than two functions. Adding or subtracting functions is always just a matter of adding/subtracting the like terms in the relationship formulas.
Adding or Subtracting Functions with the Same Input
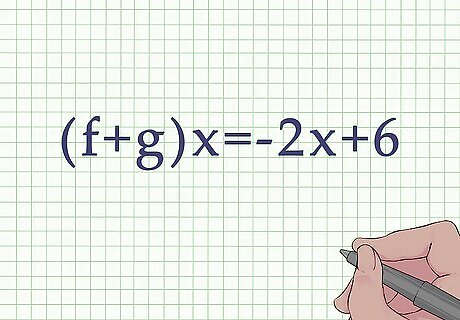
Add or subtract the functions, as described in Method 1. This will give you the formula relationship for your variable input (x). For example, you might find that ( f + g ) x = − 2 x + 6 {\displaystyle (f+g)x=-2x+6} (f+g)x=-2x+6.
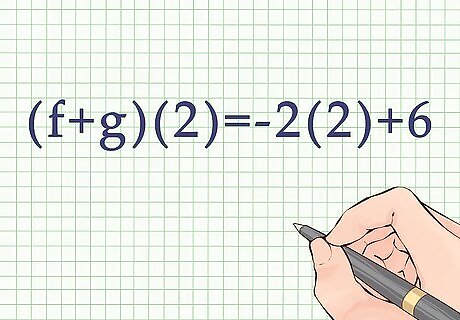
Plug in the variable. Remember, this method only works if you are adding/subtracting functions with the same input variable. For example, you might be asked to find ( f + g ) ( 2 ) {\displaystyle (f+g)(2)} (f+g)(2). Your added function would then look like ( f + g ) ( 2 ) = − 2 ( 2 ) + 6 {\displaystyle (f+g)(2)=-2(2)+6} (f+g)(2)=-2(2)+6.
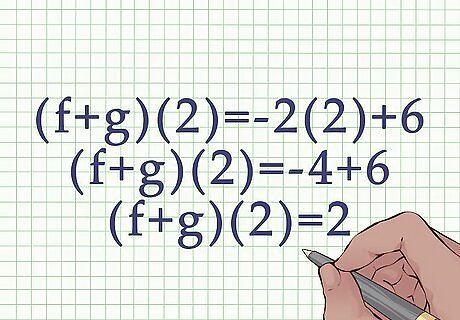
Complete the calculation. Remember to use the order of operations. For example: ( f + g ) ( 2 ) = − 2 ( 2 ) + 6 {\displaystyle (f+g)(2)=-2(2)+6} (f+g)(2)=-2(2)+6 ( f + g ) ( 2 ) = − 4 + 6 {\displaystyle (f+g)(2)=-4+6} (f+g)(2)=-4+6 ( f + g ) ( 2 ) = 2 {\displaystyle (f+g)(2)=2} (f+g)(2)=2.
Adding or Subtracting Functions with Different Inputs

Plug the appropriate variable into the first function and solve. Since you are working with two different variables (inputs), you cannot add the formulas and plug in one input, you have to complete one function at a time. For example, if you are given f ( x ) = 3 x + 2 {\displaystyle f(x)=3x+2} f(x)=3x+2 and g ( x ) = 4 − 5 x {\displaystyle g(x)=4-5x} g(x)=4-5x, and are asked to find f ( 2 ) + g ( 3 ) {\displaystyle f(2)+g(3)} f(2)+g(3), you would start by finding f ( 2 ) {\displaystyle f(2)} f(2). When you plug in the 2, you get: f ( 2 ) = 3 ( 2 ) + 2 {\displaystyle f(2)=3(2)+2} f(2)=3(2)+2 f ( 2 ) = 6 + 2 {\displaystyle f(2)=6+2} f(2)=6+2 f ( 2 ) = 8 {\displaystyle f(2)=8} f(2)=8.
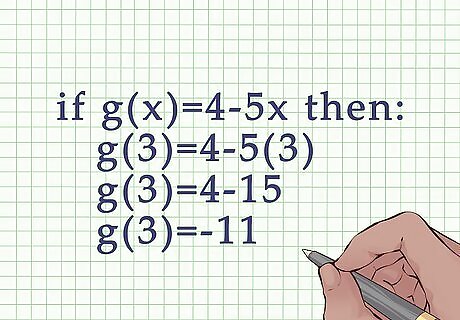
Plug the appropriate variable into the second function and solve. Make sure you are plugging in the correct variable to the correct function. For example, if g ( x ) = 4 − 5 x {\displaystyle g(x)=4-5x} g(x)=4-5x, then: g ( 3 ) = 4 − 5 ( 3 ) {\displaystyle g(3)=4-5(3)} g(3)=4-5(3) g ( 3 ) = 4 − 15 {\displaystyle g(3)=4-15} g(3)=4-15 g ( 3 ) = − 11 {\displaystyle g(3)=-11} g(3)=-11
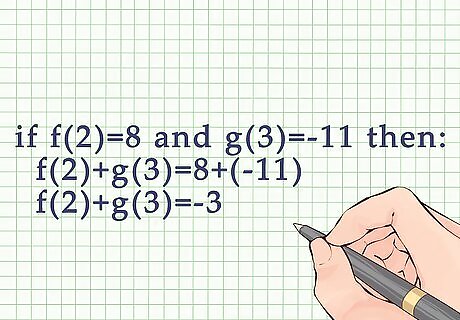
Add or subtract the two outputs. The result will be the sum or difference of the two functions, given the provided variables. For example, if f ( 2 ) = 8 {\displaystyle f(2)=8} f(2)=8 and g ( 3 ) = − 11 {\displaystyle g(3)=-11} g(3)=-11, then: f ( 2 ) + g ( 3 ) = 8 + ( − 11 ) {\displaystyle f(2)+g(3)=8+(-11)} f(2)+g(3)=8+(-11) f ( 2 ) + g ( 3 ) = − 3 {\displaystyle f(2)+g(3)=-3} f(2)+g(3)=-3.




















Comments
0 comment