2 Math Magic Tricks: Guess Someone’s 3-Digit Number or Age

The 1089 Trick

Pick a friend with decent math skills. This trick only involves addition and subtraction, but some people get confused by the instructions. It works best on a friend who will pay close attention, and who is unlikely to make a math mistake.

Write down 1089 on a hidden piece of paper. Announce that you'll write down a "magic number" on a piece of paper. Write down 1089 without showing anyone, then fold the paper in half.

Ask your friend to write down a number with three different digits. Tell him not to show you the number or tell you what it is. Make sure he understands that none of the three digits can be the same. For example, he could pick 481. He might need a simple calculator as well.

Instruct him to write down the number in reverse. On the next line underneath the number, he should write down the same digits in reverse order. For example, 481 backwards is 184.

Make it into a subtraction problem. Now that your volunteer has two numbers, have him subtract the smaller one from the larger one. 481 - 184 = 297.

If the number is only two digits, add a zero at the beginning. Now ask him if his number is two or three digits long, without telling you the actual number. If it is only two digits long, have him place a 0 at the beginning. In our example, 297 has three digits, so you can skip this step. Sometimes your friend will end up at 99, and this step will turn that into "099."

Reverse this number as well. Ask him to take his answer and reverse the digit order again. If he added the zero the beginning, remind him to include it as part of the number. For example, the reverse of 297 is 792.

Add the last number and its reverse together. As the final calculation, your friend adds the last two numbers he wrote down. In our example, 792 + 297 = 1089.

Show everyone your prediction. Announce that you know the last number he wrote down. Unfold the piece of paper and reveal the 1089 you wrote down earlier. The answer is always 1089. If your friend has a different answer, he did not follow instructions, or he made a mistake.

Guessing Age or Shoe Size

Ask a volunteer to write down her age. Give her a piece of paper and instruct her not to show you what she's writing. This trick won't work on someone 100 years old or above, but that's almost never a problem!

Have her multiply it by 5. Ask her to follow your instructions as you tell her what calculations to solve. Start by asking her to multiply her age by 5. For example, if someone is 42 years old, she would write down 42 x 5 = 210. Let her use a calculator if she'd prefer to.

Write a zero at the end of the answer. This is the same as multiplying by 10, but phrasing it this way makes it more difficult for the volunteer to follow the trick. In our example, adding a zero to 210 makes 2100.

Add today's date. It doesn't actually matter what she adds here — we'll undo it later — but today's date is an easy small number to add. Mention the date aloud to make sure she knows it. For example, if today is March 15th, the volunteer in our example would sum 2100 + 15 = 2115. Tell her to ignore the month and year.

Double the answer. The volunteer should multiply her answer by two. (This is where a calculator comes in handy.) 2115 x 2 = 4230.

Add the volunteer's shoe size. Ask the volunteer to write down her shoe size, and to round up if it's not a whole number. She should add this to her last answer. If her shoe size is 7, she'll add 4230 + 7 = 4237.

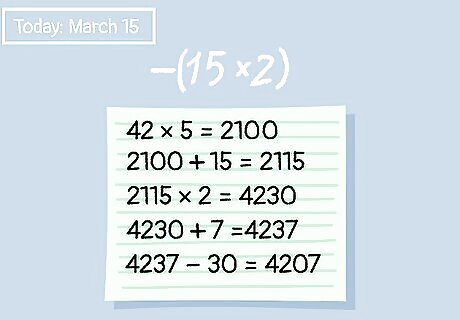
Subtract twice today's date. It's best to calculate this in your head, then tell her to subtract the number you come up with. For example, it's March 15th in our example, so multiply 15 x 2 = 30 in your head. Say "Subtract 30 from your answer" and the volunteer will calculate 4237 - 30 = 4207.

Reveal the magic. Tell her to read her answer out loud. The first part of the number is her age, and the last two digits are her shoe size.